leetcode

leetcode 例题

记录下 leetcode 值得记录的例题

kmp 算法

kmp 算法的原始实现方法在另一篇里面已经写过，实际上就是通过记录模式串的相同的前后缀长度来跳过模式串重新匹配的距离。

public int[] getNext(String pattern) {
	  int[] next = new int[pattern.length()];
		next[0] = -1;
		// 模式串相差一进行匹配
		int k = -1, j = 0;
		while (j < pattern.length() - 1) {
			  // 匹配相同的字符
				if (k == -1 || pattern.charAt(k) == pattern.charAt(j)) {
					  k++;
						j++;
						next[j] = k;
				} else {
						k = next[k];
				}
		}
		return next;
}


public int match(String s, String pattern) {
   int[] next = getNext(pattern);

   int i = 0, j = 0;
   while (i < s.length() && j < pattern.length()) {
      if (s.charAt(i) == pattern.charAt(j)) {
          i++;
          j++;
      } else {
          // 失配 重新定位
          j = next[j];
      }
   }

   if (j == pattern.length()) {
     return i - j;
   } else {
     return -1;// 没有找到
   }
}

最短回文串

给定一个字符串，问在字符串左边添加一些字母后，形成一个回文串，问形成的回文串中，最短的回文串什么。

• 超时解法

最开始的暴力思维，想得就是遍历这个字符串，找到中间可以作为分隔线的地方（因为回文串其实可以看成在一个分隔点的左右镜像），然后遍历所有的分割线，比较生成的最短回文串。

class Solution {
    // 只能在字符串前面添加
    public String shortestPalindrome(String s) {
        if (s.equals("")) return "";
        String min = null;
        // 作为 palindrome 的中心点 进行遍历
        for (int i = 0; i <= s.length() / 2; i++) {
            String odd = odd(i, s);
            String even = even(i, s);
            String tmp = "";
            if (odd.equals("") && even.equals("")) {
                continue;
            }
            if (odd.equals("")) tmp = even;
            if (even.equals("")) tmp = odd;
            if (!odd.equals("") && !even.equals("")) {
                tmp = even.length() > odd.length() ? odd: even;
            }

            if (min == null) min = tmp;
            else if (min.length() > tmp.length()) {
                min = tmp;
            }
        }
        return min;
    }

    private String odd(int i, String s) {
        int left = i - 1, right = i + 1;
        // 考虑最后的 palindrome 是奇数长度情况
        boolean canPalindrome = true;
        while (left >= 0 && right < s.length()) {
            if (s.charAt(left) != s.charAt(right)) {
                // 不能形成
                canPalindrome = false;
                break;
            }
            left--;
            right++;
        }
        String tmp = "";
        if (!canPalindrome) return tmp;

        // 左边为 -1 说明右边长要把右边的加载左边
        if (left == -1) {
            StringBuilder builder = new StringBuilder(s.substring(right));

            tmp = builder.reverse().toString() + s;
        }
        return tmp;
    }

    private String even(int i, String s) {
        int left = i - 1, right = i;
        // 考虑最后的 palindrome 是奇数长度情况
        boolean canPalindrome = true;
        while (left >= 0 && right < s.length()) {
            if (s.charAt(left) != s.charAt(right)) {
                // 不能形成
                canPalindrome = false;
                break;
            }
            left--;
            right++;
        }
        String tmp = "";
        if (!canPalindrome) return tmp;

        // 左边为 -1 说明右边长要把右边的加载左边
        if (left == -1) {
            StringBuilder builder = new StringBuilder(s.substring(right));

            tmp = builder.reverse().toString() + s;
        }
        return tmp;
    }
}

• 前后缀思维

其实考虑一个最长的回文串的，肯定是把输入串的逆向输入串拼接到原始字符串的左边。

那么，如果这个逆向的字符串有一部分跟输入串的前一部分是重合的就可以缩短整个长度。

比如

• abaaa 与其逆 aaaba 在红色的地方重合
  • 即 abaaa 的前缀 a 与 aaaba 的后缀 a 重合

所以 只需要遍历得到这个相同的前后缀即可。

下述算法，由于需要判断 equals 因此其执行效率趋近 o(n^2)

public String shortestPalindrome(String s) {
	  String reverse = new StringBuilder(s).reverse().toString();

		// 因为从后向前 可以直接返回 找到的第一个 一定是最长的相同前后缀
		for (int i = s.length(); i >= 0; i--) {
			  // 前缀等于后缀
				if (s.subString(0, i).equals(reverse.subString(s.length() - i))) {
					// 这个时候只需要加上 reverse 去除后缀的部分
					return reverse.subString(0, s.length() - i) + s;
				}
		}
		return "";
}

• kmp 思维

上面采用前后缀的方式其实已经接近了 kmp 的思维方式，不过是比较朴素的解法，因为这个时候还可以进一步得到，实际上就是求原串的最长回文前缀，因为这样逆串，反转过来后，与其回文前缀相等的部分，可以直接消去。

那么可以直接拼接成一个最长的字符串，即 s + "#" + reverse 那么只需要找到这个字符串结尾的部分相等的前后缀长度，即可以在返回结果的时候删除重复的部分。所以可用 kmp 的 next 数组求法找到最长的前后缀，既可以将时间复杂度进一步降低。

public class ShortestPalindromeNew_214 {

    // keep 春招就考的这个
    public String shortestPalindrome(String s) {
        String reverse = new StringBuilder(s).reverse().toString();

        String addedStr = s + "#" + reverse;

        int len = getMaxMatchLen(addedStr);

        return reverse.substring(0, reverse.length() - len) + s;
    }


    // 找到从末尾开始的前后缀的最长匹配长度
    public int getMaxMatchLen(String s) {
        int[] next = new int[s.length() + 1];
        next[0] = -1;
        int k = -1, j = 0;
        while (j < s.length()) {
            if (k == -1 || s.charAt(k) == s.charAt(j)) {
                k++;
                j++;
                next[j] = k;
            } else {
                k = next[k];
            }
        }
        return next[s.length()];
    }
}

单调栈

找出最具竞争力的子序列

找到其中的一个子序列，满足其字符串比较是最小的结果。

• brute-force

其实查看题意的话，最主要的就是不停的找到最小的数字

• 如果最小的数字 右侧的数字数量大于等于剩下要找的数量，说明继续向右侧寻找最小数
• 如果小于要找的数量，说明现在最小的数及其右侧所有的数字已经组成答案的一部分，因为这个最小数字形成的这个子序列一定是当前这个最小的
• 重复寻找上述过程，直到所有的数字被填充

因此上述过程是一个递归的过程（递归超时，实际上如果能够保存 i -> j 的最小值的位置的话，就不用在递归中每次寻找了，应该能节约很多时间）

// 同一个位置上的数字更小的 int[] 更具竞争力
// 问长度为 k 的 int[] 的最有竞争力的结果是什么
// 找到最小的 看后面的数 是否满足剩下的大小 不然就往前找 找到剩下的最小的
public int[] mostCompetitiveBruteForce(int[] nums, int k) {
		if (k > nums.length) return new int[k];
		if (k == nums.length) return nums;

		int[] res = new int[k];

		recursion(nums, res, 0, nums.length - 1, 0, res.length - 1);
		return res;
}

// 直接使用递归 每次找到 i->j 的最小值 然后判断去什么其他地方填充即可
public void recursion(int[] nums, int[] res, int i, int j, int n, int m) {
		if (n > m) return;
		int min = i;
		for (int k = i; k <= j; k++) {
				if (nums[k] < nums[min]) min = k;
		}
		// 剩下的数字不足以填满 m
		if (j - min + 1 <= m - n + 1) {
				for (int k = j; k >= min; k--) {
						res[m--] = nums[k];
				}
				recursion(nums, res, i, min - 1, n, m);
				return;
		}
		// 还足够填满 从剩下的里面取较小的数字 然后填满
		res[n++] = nums[min];
		recursion(nums, res, min + 1, j, n, m);
}

• 单调栈

实际上题目寻找的是最小的数字形成的结果，那么可以用一个单调栈来保存前面的访问的数组，如果当前访问的数字比之前的数字小的话，说明应该从这个数字之后开始寻找，其结果也就是把之前的数组弹出栈

public int[] mostCompetitive(int[] nums, int k) {
	if (k > nums.length) return new int[k];
	if (k == nums.length) return nums;

	int[] res = new int[k];
	// 单调栈
	Deque<Integer> stack = new LinkedList<>();

	for (int i = 0; i < nums.length; i++) {
			int num = nums[i];
			// 如果当前数字比 stack 里面的要小 说明概要弹出
			// 或者num 后剩下的长度不够了就不能弹出了
			while (!stack.isEmpty() && stack.peekLast() > num && k - stack.size() < nums.length - i) {
					stack.removeLast();
			}

			if (stack.size() < k) {
					stack.addLast(num);
			}
	}

	k--;
	while (k >= 0) {
			res[k] = stack.removeLast();
			k--;
	}
	return res;
}

下一个更大元素 II

示例
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

用单调栈来保存之前遍历过的路径，之后访问的数字如果比路径上的数字大的话，说明对于栈中保存的路径上的数字下一个更大的数是当前访问的数。

public int[] nextGreaterElements(int[] nums) {
		// 优化循环
		int n = nums.length;
		int[] res = new int[n];
		// 添加的默认值
		Arrays.fill(res, -1);
		// 单调栈保存 nums 中的下标
		Deque<Integer> stack = new LinkedList<>();
		// 因为是循环数组 所以遍历到最后一个的时候 还要看其左侧的
		// 所以相当于是两倍长度
		for (int i = 0; i < 2 * n - 1; i++) {
				// stack 里面放置的都是比 nums[i % n] 小的数 在其被弹出的时候 说明之后第一个比他大的数 就是访问的 nums[i % n]
				while (!stack.isEmpty() && nums[i % n] > nums[stack.peek()]) {
						res[stack.pop()] = nums[i % n];
				}
				stack.push(i % n);
		}
		return res;
}

移调 k 位数字

问如果在原始字符串中，移掉 k 位数字，最后形成的最小字符串是什么

1. 如果 k 大于等于原来字符串的长度，那么就相当于删除了所有的数字，直接返回 “0” 即可
2. 考虑 k 小于的情况
   • 既然要删除数字，先考虑删除一个数字的情况，如 45 中删除一个数字，那么结果就是删除5 保留4，考虑 54 也是删除5 保留4
   • 那既然如此，也就是说，从字符串中删除一个数字的话相当于删除的数字之前的一个数替代当前这位数，那么要使结果更小，替代的这个数一定要小于之前的删除的那个数，即 Dk < D(k-1) 删除 Dk

• 每次遍历删除一个数字

public String removeKdigitsDeleteOne(String num, int k) {
		// 移除所有的数字
		if (k >= num.length()) return "0";
		while (k > 0) {
				num = deleteOne(num);
				k--;
		}
		// 去除前导 0
		StringBuilder builder = new StringBuilder();
		int i = 0;
		while (i < num.length()) {
				if (num.charAt(i) != '0') break;
				i++;
		}
		while (i < num.length()) {
				builder.append(num.charAt(i++));
		}
		return builder.length() == 0 ? "0" : builder.toString();
}

private String deleteOne(String num) {
		for (int i = 1; i < num.length(); i++) {
				// 现在可以删除 i - 1 这个位置的数了
				if (num.charAt(i) < num.charAt(i - 1)) return num.substring(0, i - 1) + num.substring(i);
		}
		// 删除最后一个数字
		return num.substring(0, num.length() - 1);
}

• 单调栈

每次去删除的一个数字的时间效率太低，因此可以考虑用一个单调栈来保存小于当前数的数字，当遍历到的下标大于单调栈的尾时，说明前面的数字该删除了

public String removeKdigits(String num, int k) {
		// 移除所有的数字
		if (k >= num.length()) return "0";
		// 删除数字的话 一定要删除的是 前面一个数字 大于 后面一个数字的地方
		// 因为这样才能在删除后保证剩下的形成更小的结果
		Deque<Character> queue = new LinkedList<>();
		for (char c : num.toCharArray()) {
				// 单调栈中保存之前的结果
				while (!queue.isEmpty() && queue.peekLast() > c && k > 0) {
						queue.removeLast();
						k--;
				}
				queue.add(c);
		}

		// 剩下的 一定是一个从小到大的序列
		while (k > 0) {
				k--;
				queue.removeLast();
		}

		StringBuilder builder = new StringBuilder();

		while (!queue.isEmpty()) {
				if (queue.peekFirst() == '0') queue.removeFirst();
				else break;
		}

		while (!queue.isEmpty()) {
				builder.append(queue.removeFirst());
		}
		return builder.length() == 0 ? "0" : builder.toString();
}

滑动窗口

最小覆盖子串

滑动窗口

• 当前遍历的字符串没有包含所有字符的时候，右移右游标
• 然后左移左游标，直到不再包含该字符串
• 在移动窗口的时候不听比较即可

func checkEqualMap(mapForT, window map[int32]int) bool {
	for k, v := range mapForT {
		if count, ok := window[k]; !ok || count < v {
			return false
		}
	}
	return true
}

func minWindow(s string, t string) string {
	i, j := 0, 0
	res := ""
	mapForT := make(map[int32]int)

	for _, char := range t {
		mapForT[char]++
	}

	window := make(map[int32]int)

	for j < len(s) || i < j {
		for j < len(s) && !checkEqualMap(mapForT, window) {
			window[int32(s[j])]++
			j++
		}
		if checkEqualMap(mapForT, window) && (res == "" || len(res) > j-i) {
			res = s[i:j]
		}
		window[int32(s[i])]--
		i++
	}
	return res
}

class Solution {
    // 返回true 说明里面已经包含了一个完整的 t 字符串
    public boolean checkMap(HashMap<Character, Integer> mapForT, HashMap<Character, Integer> mapForS) {
        for (Character key : mapForT.keySet()) {
            if (!mapForS.containsKey(key) || mapForS.get(key) < mapForT.get(key)) return false;
        }
        return true;
    }

    public String minWindow(String s, String t) {
        // 这都是不存在的
        if (s == null || t == null || s.length() < t.length()) return "";
        String minStr = null;
        HashMap<Character, Integer> mapForT = new HashMap<>();
        for (char character : t.toCharArray()) {
            if (!mapForT.containsKey(character)) {
                mapForT.put(character, 1);
            } else {
                mapForT.put(character, mapForT.get(character) + 1);
            }
        }

        HashMap<Character, Integer> mapForS = new HashMap<>();
        for (int i = 0; i < t.length(); i++) {
            Character character = s.charAt(i);
            if (!mapForS.containsKey(character)) {
                mapForS.put(character, 1);
            } else {
                mapForS.put(character, mapForS.get(character) + 1);
            }
        }
        // 滑动窗口大小
        int left  = 0, right = t.length() - 1;
        do {
            while (checkMap(mapForT, mapForS) && right - left + 1 >= t.length()) {
                if (minStr == null || minStr.length() > right - left + 1) {
                    minStr = s.substring(left, right + 1);
                }
                mapForS.put(s.charAt(left), mapForS.get(s.charAt(left)) - 1);
                left++;
            }
            right++;
            if (right >= s.length()) continue;
            if (!mapForS.containsKey(s.charAt(right))) {
                mapForS.put(s.charAt(right), 1);
            } else {
                mapForS.put(s.charAt(right), mapForS.get(s.charAt(right)) + 1);
            }
        } while (right <= s.length() - 1 && right - left + 1 > t.length());
        return minStr == null ? "" : minStr;
    }
}

K 个不同整数的子数组

找到 A 里面的连续子数组，其中子数组里面的数据的 distinct 只有 K 个

这个题目一想就是滑动窗口

但是 很不好计算 等于 K 的时候 数组有多少个

但是计算 小于等于 K 的比较好计算，可以依据以下规则

以 [1,2,1,2,3] 为例，左边界固定的时候，恰好存在 2 个不同整数的子区间为 [1,2],[1,2,1],[1,2,1,2]，总数为 3。其值为下标 3 - 1 + 1，即区间 [1..3] 的长度。

因为，left, right 同时圈定了一组满足 <= k 的题意的长度范围

那么，包含 left 的子数组数量肯定是 right - left + 1，因为相当于每次给数组里面添加一个数([1,2] [1,2,1] [1,2,1,2]) 所以 right 比 left 多几个数 就能形成几个子数组

func subarraysWithKDistinct(A []int, K int) int {
	return atMostK(A, K) - atMostK(A, K-1)
}

// 因为求解 恰好K 不好弄 求解 最大K 比较好弄
func atMostK(A []int, K int) int {
	i, j := 0, 0
	// 作为一个 set 保存窗口内的所有 distinct 数据
	window := make(map[int]int)
	res := 0

	for j < len(A) {
		window[A[j]]++
		j++

		for len(window) > K {
			window[A[i]]--
			if window[A[i]] == 0 {
				delete(window, A[i])
			}
			i++
		}

		res += j - i + 1
	}

	return res
}

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;

public class SubarraysWithKDistinct_992 {

    // 如果 A 里面
    public int subarraysWithKDistinct(int[] A, int K) {
        return subArraysDistinctAtMostK(A, K) - subArraysDistinctAtMostK(A, K - 1);
    }

    // 计算最多的有多少个的话 可以固定左边界 然后计算
    private int subArraysDistinctAtMostK(int[] array, int k) {
        Map<Integer, Integer> window = new HashMap<>();

        int res = 0;

        int left = 0, right = 0;

        while (right < array.length) {
            // 固定左边界 移动右边界
            window.put(array[right], window.getOrDefault(array[right], 0) + 1);
            // 这边已经需要减除了
            while (left <= right && window.size() > k) {
                window.put(array[left], window.get(array[left]) - 1);
                if (window.get(array[left]) == 0) window.remove(array[left]);
                left++;
            }
            // 这个地方是因为右边界到左边之间的数字 一定是小于等于 K 个不同的数字的
            // 那么能够以左边界形成的 一定是中的一个子数组 如
            // 以 [1,2,1,2,3] 为例，左边界固定的时候，恰好存在 2 个不同整数的子区间为 [1,2],[1,2,1],[1,2,1,2]，总数为 3。其值为下标 3 - 1 + 1，即区间 [1..3] 的长度。
            res += right - left;
            right++;
        }

        return res;
    }

    public static void main(String[] args) {
        System.out.println(new SubarraysWithKDistinct_992().subarraysWithKDistinct(new int[]{1,2,1,2,3}, 2));
        System.out.println(new SubarraysWithKDistinct_992().subarraysWithKDistinct(new int[]{1,2,1,3,4}, 3));
    }
}

最大连续 1 的个数 III

最大连续 1 的个数，A 中只有 0 和 1，其中可以变换最多 K 个 0 成为 1，问最长的连续 1 的长度为多少

滑动窗口，窗口中最多含有 K 个 0 即可

func longestOnes(A []int, K int) int {
	// 返回值
	res := 0
	left, right := 0, 0
	zeros := 0
	for right < len(A) {
		// 用外层循环带动 right 移动
		if A[right] == 0 {
			zeros++
		}
		// 这个时候要移动左侧的 left 保障 zeros 小
		for zeros > K {
			if A[left] == 0 {
				zeros--
			}
			left++
		}
		// 每轮都去比较即可
		res = max(res, right - left + 1)
		right++
	}
	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

绝对差不超过限制的最长连续子数组

给定一个数组 nums 和 limit，找到最长的连续数组，其中任意两个数的差值不超过 limit

上面这句话换个说法说的就是 最大值和最小值 之差不超过 limit，因此如果能够 o(1) 的拿到窗口的 最大最小值，那么就比较方便

package classic

type MaxMinQueue struct {
	stack1 MaxMinStack
	stack2 MaxMinStack
}

func (queue *MaxMinQueue) Push(val int) {
	queue.stack1.Push(val)
}

func (queue *MaxMinQueue) Shift() int {
	if queue.stack2.Len() == 0 {
		for queue.stack1.Len() > 0 {
			queue.stack2.Push(queue.stack1.Pop())
		}
	}
	return queue.stack2.Pop()
}

func (queue *MaxMinQueue) Max() int {
	if queue.stack1.Len() == 0 {
		return queue.stack2.Max()
	} else if queue.stack2.Len() == 0 {
		return queue.stack1.Max()
	}
	return max(queue.stack2.Max(), queue.stack1.Max())
}

func (queue *MaxMinQueue) Min() int {
	if queue.stack1.Len() == 0 {
		return queue.stack2.Min()
	} else if queue.stack2.Len() == 0 {
		return queue.stack1.Min()
	}
	return min(queue.stack2.Min(), queue.stack1.Min())
}

func (queue *MaxMinQueue) Len() int {
	return queue.stack1.Len() + queue.stack2.Len()
}

type MaxMinStack struct {
	// 这两个不用 slice 用 list 之类的链表 可能会快一点儿
	data  []int
	maxes []int
	mins  []int
}

func (ms *MaxMinStack) Push(val int) {
	ms.data = append(ms.data, val)
	if len(ms.maxes) > 0 {
		ms.maxes = append(ms.maxes, max(ms.maxes[len(ms.maxes)-1], val))
	} else {
		ms.maxes = append(ms.maxes, val)
	}

	if len(ms.mins) > 0 {
		ms.mins = append(ms.mins, min(ms.mins[len(ms.mins)-1], val))
	} else {
		ms.mins = append(ms.mins, val)
	}
}

func (ms *MaxMinStack) Pop() int {
	res := ms.data[len(ms.data)-1]
	ms.data = ms.data[:len(ms.data)-1]
	ms.maxes = ms.maxes[:len(ms.maxes)-1]
	ms.mins = ms.mins[:len(ms.mins)-1]
	return res
}

func (ms *MaxMinStack) Max() int {
	return ms.maxes[len(ms.maxes)-1]
}

func (ms *MaxMinStack) Min() int {
	return ms.mins[len(ms.mins)-1]
}

func (ms *MaxMinStack) Len() int {
	return len(ms.data)
}

// 找到一个最长的连续子数组 其任意两个元素之间的差值 小于等于 limit
func longestSubarray(nums []int, limit int) int {
	// 就是维护一个 queue 为了方便 应该在 o(1) 的时间内获得其 最大最小值
	left, right := 0, 0
	window := &MaxMinQueue{stack1: MaxMinStack{}, stack2: MaxMinStack{}}
	res := 0
	for right < len(nums) {
		window.Push(nums[right])
		if window.Len() > 0 && window.Max() - window.Min() <= limit {
			res = max(res, right - left + 1)
		}

		for window.Len() > 0 && window.Max() - window.Min() > limit {
			window.Shift()
			left++
		}
		right++
	}
	return res
}

爱生气的书店老板

给定一个 grumpy 以及 custormers 在 grumpy == 0 的时候 可以加上 custormers 的对应值，问如果有连续的 X 个 gurmpy 可以为 0 最大 customers 的和为多少

• 自己的做法

维护一个前缀和数组 sum，表示前 i 个的和为多少，那么就可以用滑动窗口将数组分为三段

[0->l](可以用 sum 数组求得) [l->r](全部变为 0 所以是直接求和的) [r->len](可以用 sum 数组求得)

public int maxSatisfiedWithSumArray(int[] customers, int[] grumpy, int X) {
		// sum[i] 保存 customers[i] 之前的所有满足要求的和
		int[] sum = new int[customers.length + 1];

		for (int i = 1; i <= customers.length; i++) {
				sum[i] = sum[i - 1];
				if (grumpy[i - 1] == 0) {
						sum[i] += customers[i - 1];
				}
		}
		// 结果
		int res = 0;
		// 维护一个窗口 这个窗口长度为 X 全部认为是可以加的
		int windowSum = 0;
		for (int i = 0; i < X; i++) {
				windowSum += customers[i];
		}
		for (int i = X; i < customers.length; i++) {
				res = Math.max(res, sum[i-X] + windowSum + sum[customers.length] - sum[i]);
				windowSum = windowSum - customers[i - X] + customers[i];
		}
		res = Math.max(res, sum[customers.length-X] + windowSum);
		return res;
}

• 题解

题解更进一步，将 customers 数组根据 grumpy 的取值分为两类，一类是 grumpy 等于 1 那么是可以直接加上的，一类是 grumpy == 0，可以在长度为 X 的滑动窗口中 increase 到 第一类的

public int maxSatisfied(int[] customers, int[] grumpy, int X) {
		// 分两步计算 一个计算满足要求的所有和 total 另一个窗口可以额外增加的值
		int total = 0;
		for (int i = 0; i < customers.length; i++) {
				// grumpy[i] == 0 的时候 才加上
				total += (1 - grumpy[i]) * customers[i];
		}
		// 遍历可以增加的值 找到最大的
		int window = 0;
		// 窗口遍历可以增加的值
		for (int i = 0; i < X; i++) {
				// 窗口可以增加的值 是 grumpy[i] == 1
				window += grumpy[i] * customers[i];
		}
		int res = window;
		for (int i = X; i < customers.length; i++) {
				window = window - grumpy[i-X] * customers[i-X] + grumpy[i] * customers[i];
				res = Math.max(res, window);
		}
		return total + res;
}

二进制题目

连接连续二进制数字

题目要求的是将 1 -> n 的二进制的字符拼接起来表示一个超大的二进制数，然后将 二进制 数转换成为 十进制 数，并模上 1000000007。

如果直接把每个数字转换成为二进制数，然后拼接转换，因为会超时，因为 n 的返回达到了 10^5。

所以考虑在遍历的时候直接对每一位数进行处理。

观察事例，可以看到其实相当于 1(1) << 4 位数 10(2) << 2 11(3) 不变，所以只需要在每个数字遍历的时候，将上一个数字形成的结果左移当前数字对应的二进制的位数的长度，加上该数即可

n = 3, res = 27
二进制表示为 1 -> 1, 2 -> 10, 3 -> 11
27 二进制表示为 11011

计算二进制数的长度的时候，可以简单的采用遍历的方式进行。

• [1] 一位数长度
• [2,3] 二位数长度
• [4,……,7] 三位数长度
• [8,……,15] 四位数长度

也就是说，长度也是一个可以从上一个长度推断来的，每次需要新增长度的时候，都是形成 2 的幂 的形成，可以用 i & (i - 1) 来快速的判断 2 的幂。

private static int mod = 1000000007;

// 只需要知道遍历的 n 的位数的长度即可
public int concatenatedBinary(int n) {
		long res = 0;
		int shift = 0;
		// 因为要返回的是 1 - n 的数字的二进制的组合形成的大数字的十进制数
		// 比如 1 2 3 组成的 1 10 11 返回 27
		// 相当于 首先访问 1 结果为 1
		// 访问 2 然后 1 左移两位 再加上 2
		// 访问 3 上一步的结果 再左移两位 加上 3
		// 所以对于每一个数字来说 实际上只需要让上一次的结果 不停的左移它的二进制的位数长度即可
		for (int i = 1; i <= n; i++) {
				// 因为二的幂次方为 1000 的形式
				// 所以一旦知道现在的 i 为 2 的幂次方 就需要 shift++
				if ((i & (i - 1)) == 0) {
						shift++;
				}
				res = ((res << shift) + i) % mod;
		}
		return (int) res;
}

模拟除法

不能使用乘法、除法和 mod 运算符。

除法的本质，以 10 / 3 为例

10 / 3 = 3 …… 1 (即为 3 个 3 相乘 余 1)

即为 10 - (3 _ 2) - (3 _ 1) = 1 其结果为 2 + 1 为 3

也就是说任意一种除法可以用一组除数的 2 的次方的乘积的结果来表示。

如 100 / 15 = 6

100 - (15 _ 4) - (15 _ 2)

所以可以采用二进制的方法来做，每次用被除数减去最大的一个除数的 2 次方的乘积，循环，直到剩下余数或者 0

func divide(dividend int, divisor int) int {
	if divisor == 0 {
		return 1 << 31 - 1
	}
	minus := -1
	if (dividend < 0 && divisor < 0) || (dividend > 0 && divisor > 0) {
		minus = 1
	}

	absDividend, absDivisor := int64(math.Abs(float64(dividend))), int64(math.Abs(float64(divisor)))
	res := 0
	for absDividend >= absDivisor {
		tmp, multi := absDivisor, 1
		for (tmp << 1) < absDividend {
			tmp <<= 1
			multi <<= 1
		}
		absDividend -= tmp
		res += multi
		if minus > 0 && res >= math.MaxInt32 {
			return math.MaxInt32
		} else if minus < 0 && minus * res <= math.MinInt32 {
			return  math.MinInt32
		}
	}
	return minus * res
}

class Solution {
    public int divide(int dividend, int divisor) {
        if(divisor == 0 || (dividend == Integer.MIN_VALUE && divisor == -1)) return Integer.MAX_VALUE;

        int sign;
        if ((dividend > 0 && divisor > 0) || (dividend < 0 && divisor < 0)) sign = 1;
        else sign = -1;

        int res = 0;

        long dvd=Math.abs((long)dividend);
        long dvs=Math.abs((long)divisor);
        while (dvd >= dvs) {

            long temp = dvs, m = 1;
            while (temp << 1 < dvd) {
                temp <<= 1;
                m <<= 1;
            }

            res += m;
            dvd -= temp;

        }
        return sign * res;
    }
}

只出现一次的数字 II

数组中的数组只有出现 1 次（一个数字）的和 3 次的数字，找到只出现一次的那个数字

其实就是计算每一位数字出现的次数 % 3

注意 goland 默认的 int 可能值得是 int64 所以强制指定为 32 为长度的 int32 不然没办法处理负数的情况

func singleNumber(nums []int) int {
	var res int32

	for i := 0; i < 32; i++ {
		var count int32
		for _, num := range nums {
			count += (int32(num )>> i) & 1
		}
		res += (count % 3) << i
	}
	return int(res)
}

只出现一次的数字 III

一组数字 其中只有两个数字 出现一次 其余出现两次

func singleNumberIII(nums []int) []int {
	// 如果两个出现一次的数 不同 肯定不为 0
	sum := 0

	for _, num := range nums {
		sum ^= num
	}

	// 那么根据 sum 的某一个不为 0 的位数来分离两类数
	counter := 1
	for sum & 1 == 0 {
		sum >>= 1
		counter <<= 1
	}

	// 找到了这个位数 根据 位数 分成两组即可
	num1, num2 := 0, 0

	for _, num := range nums {
		// 根据位数分离两类数
		if num & counter == 0 {
			num1 ^= num
		} else {
			num2 ^= num
		}
	}
	return []int{num1, num2}
}

数字按位与

要求求 m -> n 的范围内的所有数字的 按位与 的结果，因为范围比较大，直接 & 会超时

考虑 3 -> 11 这个范围的数字，红色的 就是相同的二进制前缀部分 实际上就是找到这部分前缀

001011      11
001010      10
001001      09
001000      08
000111      07
000110      06
000101      05
000100      04
000011      03

func rangeBitwiseAnd(m int, n int) int {
	if m == n {
		return m
	}
	// 考虑 [5,6,7] 三个数 & 起来的话 实际上是 考虑 最大值 和 最小值的 左侧相等的部分是多少
	// mov 记录移位了多少次 然后再移动回来
	mov := 0
	for m != n {
		m >>= 1
		n >>= 1
		mov++
	}

	return m << mov
}

动态规划

最后一块石头的重量 II

其实就是问是否能够形成相等的两部分, 用一个 dp[i][j] 表示前 i 个的能否形成和为 j 的数值，在遍历的时候就可以找到最大的和为多少，之后就减去最大的和即可

package classic

// 这道题题干 要求 stones 两两相撞 剩下一块儿 为剩下的石头 最小能形成的重量
// 其实就是问是否能够形成相等的两部分 因为相等的话 最后形成的石头 为 0
func lastStoneWeightII(stones []int) int {
	sum := getStonesSum(stones)
	// dp[i][j] 表示前 i 个能否形成 何为 j
	dp := make([][]bool, len(stones)+1)
	for i := 0; i < len(dp); i++ {
		dp[i] = make([]bool, sum/2+1)
		// 合为0一定可以
		dp[i][0] = true
	}
	maxSum := 0
	for i := 1; i <= len(stones); i++ {
		for j := 1; j <= sum/2; j++ {
			// 因为表示的前 i 能不能形成 j 所以 i-1 能形成的话 也是可以的
			dp[i][j] = dp[i][j] || dp[i-1][j]
			if j >= stones[i-1] {
				dp[i][j] = dp[i][j] || dp[i-1][j-stones[i-1]]
			}
			if dp[i][j] {
				maxSum = max(maxSum, j)
			}
		}
	}
	return sum - 2 * maxSum
}

func getStonesSum(stones []int) (sum int) {
	for _, w := range stones {
		sum += w
	}
	return
}

最长子序列套题

最长上升子序列

找到非连续的递增子序列，那么我就只需要知道 在我之前的小于我的数字的上升子序列长度为多少

即实际上只需要在访问数组的时候 0 ≤ i < j < nums.length，只需要知道 i 下标对应的最长的子序列是多少即可。

这样就变成了一个 dp 问题，小问题就是解决的以 nums[i] 结尾的最长的上升子序列的长度

func lengthOfLIS(nums []int) int {
	// dp[i] 表示 nums[i] 结尾的最长的递增子序列长度为多少
	dp := make([]int, len(nums))
	// 初始化 一个数字肯定是递增的
	for i := 0; i < len(nums); i++ {
		dp[i] = 1
	}
	res := 0
	for i, num := range nums {
		for j := 0; j < i; j++ {
			if num > nums[j] {
				dp[i] = max(dp[i], dp[j]+1)
			}
		}
		res = max(res, dp[i])
	}
	return res
}

最长上升子序列数量

与上面那个类似 也是一个 dp 问题 只是需要在 dp 遍历的时候 知道 对应最长长度 对应的 LIS 有多少个

// 找到 LIS 对应的长度的子序列有多少个
func findNumberOfLIS(nums []int) int {
	// 保存 nums[i] 结尾的 LIS 的长度
	dp := make([]int, len(nums))
	// 保存 nums[i] 结尾的 LIS 的最长 LIS 的长度
	counts := make([]int, len(nums))
	// 初始化
	for i := 0; i < len(dp); i++ {
		dp[i] = 1
		counts[i] = 1
	}

	maxLen := 0
	for i := 0; i < len(nums); i++ {
		for j := 0; j < i; j++ {
			// 形成 递增
			if nums[j] < nums[i] {
				if dp[i] <= dp[j] {
					// 说明 j 的长度比这个长
					dp[i] = dp[j] + 1
					counts[i] = counts[j]
				} else if dp[j]+1 == dp[i] {
					// 长度相差 1 说明这个时候 counts 要 + 上 j 的
					counts[i] += counts[j]
				}
			}
		}
		maxLen = max(maxLen, dp[i])
	}

	res := 0
	for i, count := range counts {
		if maxLen == dp[i] {
			res += count
		}
	}
	return res
}

摆动序列

找到摆动序列（摆动序列是一升一降的序列，即前后相减为一正一负）参考注释即可 (这个题目不要求连续 所以还需要不停的保存前一个状态 不用初始化)

// 两个数组分别代表上升和下降序列的最大长度
// 因为 wiggle 的数组 是一升一降 的 up[i] 表示 最后一个 nums[i] 是上升的趋势的最大值
func wiggleMaxLengthWithoutMemo(nums []int) int {
	if len(nums) == 0 {
		return 0
	}
	// up[i] down[i] 分别代表上升和下降序列(最后一个是上升或者下降)的 在 index = i 时的最长长度
	ups, downs := make([]int, len(nums)), make([]int, len(nums))
	// 初始化
	ups[0] = 1
	downs[0] = 1
	for i := 1; i < len(nums); i++ {
		if nums[i] > nums[i-1] {
			// 如果 nums i 是上升趋势 说明那么 之前前一个是下降的趋势的话 可以 加一
			// 同时 也可以不考虑这个 上升趋势 跟前一个比较
			ups[i] = max(downs[i-1]+1, ups[i-1])
			// 此时由于是上升的 所以没有下降的趋势 状态直接转移
			downs[i] = downs[i-1]
		} else if nums[i] < nums[i-1] {
			downs[i] = max(ups[i-1]+1, downs[i-1])
			ups[i] = ups[i-1]
		} else {
			// 相等的情况下是不变的
			ups[i] = ups[i-1]
			downs[i] = downs[i-1]
		}
	}
	return max(ups[len(ups)-1], downs[len(downs)-1])
}

因为只依赖前一个状态 因此可以压缩状态

// 两个数组分别代表上升和下降序列的最大长度
// 因为 wiggle 的数组 是一升一降 的 up[i] 表示 最后一个 nums[i] 是上升的趋势的最大值
func wiggleMaxLength(nums []int) int {
	if len(nums) == 0 {
		return 0
	}
	up, down := 1, 1

	for i := 1; i < len(nums); i++ {
		preDown, PreUp := down, up
		if nums[i] > nums[i-1] {
			up = max(down+1, up)
			down = preDown
		} else if nums[i] < nums[i-1] {
			down = max(up+1, down)
			up = PreUp
		} else {
			up = PreUp
			down = preDown
		}
	}
	return max(up, down)
}

类似摆动序列的题目 978. 最长湍流子数组

找到一个连续的子数组能够满足

当 A  的子数组  A[i], A[i+1], …, A[j]  满足下列条件时，我们称其为湍流子数组：

若  i <= k < j，当 k  为奇数时， A[k] > A[k+1]，且当 k 为偶数时，A[k] < A[k+1]；
或 若  i <= k < j，当 k 为偶数时，A[k] > A[k+1] ，且当 k  为奇数时， A[k] < A[k+1]。
也就是说，如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是湍流子数组。

func maxTurbulenceSize(arr []int) int {
	// 仍然是一升一降 才能使符号反号

	up, down := 1, 1
	res := 1
	for i := 1; i < len(arr); i++ {
		if arr[i] > arr[i-1] {
			up = down+1
			// 因为是要连续的 一升一降 所以这个地方需要重新初始化为 1
			down = 1
		} else if arr[i] < arr[i-1] {
			down = up + 1
			up = 1
		} else {
			up, down = 1, 1
		}
		// 因为重新初始化 所以需要对每一个状态进行比较保存
		res = max(res, max(up, down))
	}

	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

俄罗斯套娃信封问题

根据信封的宽度和高度 判断能够装下的信封的最大长度有多少

高度和宽度均小于另外一个信封的 可以装进去

实际上是一个 找到最长递增序列的问题

• 按照宽度进行排序，这样从一个维度上看 所有的信封都是宽度有序的
• 再次基础上 如果要前一个信封能够装在后一个信封里面 说明长度是一个逆序的
• 最后只需要在这个排序的数组里面 找到长度的一个最长递增序列即可

func maxEnvelopes(envelopes [][]int) int {
	// envelopes[0] 相等 说明宽度相等 这个时候 只需要更长的排在后面即可
	// envelopes[0] 不等 说明宽度不等 这个时候 只需要只需要根据长度大小从大到小排序即可
	sort.Slice(envelopes, func(i, j int) bool {
		if envelopes[i][0] == envelopes[j][0] {
			return envelopes[i][1] > envelopes[j][1]
		} else {
			return envelopes[i][0] < envelopes[j][0]
		}
	})

	// 因为现在这样排序之后 信封的宽度 一定是满足顺序的 那么只需要判断长度 能够形成的最长的递增子序列是多长
	dp := make([]int, len(envelopes))
	// 1 个数字也能有一个长度
	for i := 0; i < len(dp); i++ {
		dp[i] = 1
	}

	res := 0
	for i := 0; i < len(dp); i++ {
		tmp := 0
		for j := 0; j < i; j++ {
			if envelopes[i][1] > envelopes[j][1] {
				tmp = max(tmp, dp[j])
			}
		}
		dp[i] = tmp + 1
		res = max(res, dp[i])
	}

	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

解码方法

这道题是入门的动态规划 只要知道 前一个和前前个的状态，就可以转移到下一个状态

func numDecodings(s string) int {
	if len(s) == 0 {
		return 0
	}
	// dp[i] 表示 s[0:i] 不包括i能生成的数量
	// dp[i] = dp[i-1]+dp[i-2]
	// 因为只要当前的这个 sting 能够被 decoding 说明只要加上前面的数量即可
	dp := make([]int, len(s) + 1)
	dp[0] = 1
	// 表示的每次遍历的string的尾部
	for i := 1; i <= len(s); i++ {
		for j := max(i - 2, 0); j < i; j++ {
			if canDecoding(s[j:i]) {
				dp[i] += dp[j]
			}
		}
	}
	return dp[len(s)]
}

func canDecoding(s string) bool {
	if len(s) > 1 && s[0] == '0' {
		return false
	}

	if num, err := strconv.Atoi(s); err != nil || num > 26 || num < 1 {
		return false
	}
	return true
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

子序列

不同的子序列

func numDistinct(s string, t string) int {
	// dp[i][j] 表示 s[i-1] 和 t[j-1] 之间有多少组合
	dp := make([][]int, len(s)+1)
	for i := 0; i <= len(s); i++ {
		dp[i] = make([]int, len(t)+1)
	}

	// 初始化 只要 t 是空 那么一定可以 在 s 中找到
	for i := 0; i <= len(s); i++ {
		dp[i][0] = 1
	}

	for i := 1; i <= len(s); i++ {
		for j := 1; j <= len(t); j++ {
			if s[i-1] == t[j-1] {
				// 分为两个部分 因为可以不算当前的 s 串的最后一个 也可以算上
				// 因为 s 串的前面部分 可能已经匹配到了
				dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
			} else {
				dp[i][j] = dp[i-1][j]
			}
		}
	}

	return dp[len(s)][len(t)]
}

打家劫舍系列题

打家劫舍 I

这道题是经典的 dp 问题。题目要求的是不能抢劫相邻的位置，那么这种条件下的最大和是多少。

• 一个位置会有两个状态，拿当前这个地方的值 或者 不拿
• 下个位置的状态就会由上一个位置决定
  • 如果当前位置拿了值的话，上一个位置只能不拿
  • 如果当前位置没有拿，上一个位置只需要取拿 or 不拿的 较大值

优化下 dp 数组 其实可以用一对值表示前面一个循环中拿了的最大值即可

func rob(nums []int) int {
	if len(nums) <= 0 {
		return 0
	}
	// 优化的目的在于去掉数组 因为现在直接最大的就是
	notRob, rob := 0, 0
	res := 0

	for _, num := range nums {
		rm := rob
		rob = notRob + num
		notRob = max(notRob, rm)
		res = max(notRob, rob)
	}
	return res
}

打家劫舍 II

这个是打劫的循环数组，因为 rob 了第一个 就不能 rob 最后一个

所以分别访问从 [1:len(nums)] 和 [0:len(nums)-1] 然后比较大小即可

func rob(nums []int) int {
	if len(nums) <= 0 {
		return 0
	}
	if len(nums) == 1 {
		return nums[0]
	}
	// 因为是首尾相连的
	robFirst := getMaxRob(nums[:len(nums)-1])
	notRobFirst := getMaxRob(nums[1:])
	return max(robFirst, notRobFirst)
}

func getMaxRob(nums []int) int {
	notRob, rob := 0, 0
	res := 0

	for _, num := range nums {
		rem := rob
		rob = notRob + num
		notRob = max(rem, notRob)
		res = max(res, max(rob, notRob))
	}
	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

打家劫舍 III

这次是树，实际上还是要知道子节点上的话 rob 和 notRob 的状态即可，然后递推到当前的状态

func rob(root *TreeNode) int {
	var res int
	recursionRobTree(root, &res)
	return res
}

// recursionRobTree 返回值是 rob 当前这个 root 还不 不 rob 的值
func recursionRobTree(root *TreeNode, res *int) (int, int) {
	if root == nil {
		return 0, 0
	}

	leftRob, leftNotRob := recursionRobTree(root.Left, res)
	rightRob, rightNotRob := recursionRobTree(root.Right, res)

	// 如果 rob 当前这个root 节点的话 意味着 两个节点都不可以rob
	rob := leftNotRob + rightNotRob + root.Val
	// 如果 不 rob 这个节点的话 子节点可以 rob 也可以不 rob
	notRob := getArrayMax(leftRob + rightRob, rightRob + leftNotRob, rightNotRob + leftRob, rightNotRob + leftNotRob)
	*res = max(*res, rob)
	*res = max(*res, notRob)
	return rob, notRob
}

func getArrayMax(nums ...int) int {
	if len(nums) == 0 {
		return -1
	}
	res := nums[0]
	for _, num := range nums {
		res = max(res, num)
	}
	return res
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

贪心算法

转换罗马字

package classic

import (
	"strings"
)

var (
	memo = make(map[int]string)
	keys []int
)

func init() {
	memo[1] = "I"
	memo[4] = "IV"
	memo[5] = "V"
	memo[9] = "IX"
	memo[10] = "X"
	memo[40] = "XL"
	memo[50] = "L"
	memo[90] = "XC"
	memo[100] = "C"
	memo[400] = "CD"
	memo[500] = "D"
	memo[900] = "CM"
	memo[1000] = "M"

	keys = []int{1000,900,500,400,100,90,50,40,10,9,5,4,1}
}

func intToRoman(num int) string {
	res := strings.Builder{}

	for _, key := range keys {
		for num >= key {
			res.WriteString(memo[key])
			num -= key
		}
	}
	return res.String()
}

jumpGame

func canJump(nums []int) bool {
	rightMost := 0
	for i, num := range nums {
		// 如果当前的下标大于 rightMost 说明这个点是无法到达的 直接返回 false 即可
		if i > rightMost {
			return false
		}
		// 维护一个能够到达的最远距离
		rightMost = max(rightMost, i + num)
		// 最远距离大于长度 即可知道能够达到
		if rightMost >= len(nums) - 1 {
			return true
		}
	}
	return false
}

递归

执行乘法运算的最大分数

给你两个长度分别 n 和 m 的整数数组 nums 和 multipliers ，其中 n >= m ，数组下标 从 1 开始 计数。
初始时，你的分数为 0 。你需要执行恰好 m 步操作。在第 i 步操作（从 1 开始 计数）中，需要：
选择数组 nums 开头处或者末尾处 的整数 x 。
你获得 multipliers[i] * x 分，并累加到你的分数中。
将 x 从数组 nums 中移除。
在执行 m 步操作后，返回 最大 分数。

• 暴力解法

暴力解法就是直接根据每次取的不同字符生成一颗二叉树，然后在二叉树上进行遍历得到结果

class Solution {
    public int maximumScore(int[] nums, int[] multipliers) {
        Deque<Integer> num = new LinkedList<>();
        for (int t : nums) {
            num.addLast(t);
        }
        return recursion(0, multipliers, num);
    }

    public int recursion(int index, int[] multipliers, Deque<Integer> nums) {
        if (index >= multipliers.length) return 0;
        Deque<Integer> tmp = new LinkedList<>(nums);
        return Math.max(multipliers[index] * nums.removeFirst() + recursion(index + 1, multipliers, nums),
                multipliers[index] * tmp.removeLast() + recursion(index + 1, multipliers, tmp));
    }
}

• 带 memo

观察上述的结果的话，可以首先进行的优化是去除 dequeue 的使用，直接使用一个范围框定 nums 的选取

public int maximumScore(int[] nums, int[] multipliers) {
		return recursion(0, multipliers, nums, 0, nums.length - 1);
}

public int recursion(int index, int[] multipliers, int[] nums, int left, int right) {
		if (index >= multipliers.length) return 0;
		int l = nums[left] * multipliers[index] + recursion(index + 1, multipliers, nums, left + 1, right, memo);
		int r = nums[right] * multipliers[index] + recursion(index + 1, multipliers, nums, left, right - 1, memo);
		return Math.max(l, r);
}

但是上述的方法仍然超时，因为遍历这颗形成的二叉树的时候，会有重复的访问情况，可以观察到的是 left + n - 1 - right == index，因为从左边选取的数字数量和右边选取的数字的数量，肯定是 multipliers 选取的数量。

public int maximumScore(int[] nums, int[] multipliers) {
		// 上面的 left、right、index 其实可以用任意两个来表示即可
		// 因为可以根据公式互换，所以这样选择的 memo 是最小的
		int[][] memo = new int[multipliers.length][multipliers.length];
		for (int i = 0; i < multipliers.length; i++) {
				Arrays.fill(memo[i], Integer.MAX_VALUE);
		}
		return recursion(0, multipliers, nums, 0, nums.length - 1, memo);
}

// 因为 left + n - 1 - right == index
// 因为其结果代表的是 左边选取 left 个 右边选取 n - 1 - right 个
// 而取出的结果
public int recursion(int index, int[] multipliers, int[] nums, int left, int right, int[][] memo) {
		if (index >= multipliers.length) return 0;
		if (memo[left][index] != Integer.MAX_VALUE) return memo[left][index];
		int l = nums[left] * multipliers[index] + recursion(index + 1, multipliers, nums, left + 1, right, memo);
		int r = nums[right] * multipliers[index] + recursion(index + 1, multipliers, nums, left, right - 1, memo);
		memo[left][index] = Math.max(l, r);
		return memo[left][index];
}

括号生成

// generateParenthesis 入口函数
func generateParenthesis(n int) []string {
	res := make([]string, 0)
	recursionGenerate(&res, "", n, n)
	return res
}

// 递归生成
func recursionGenerate(res *[]string, tmp string, left, right int) {
	if left == 0 && right == 0 {
		*res = append(*res, tmp)
		return
  }
  // 由于左括号可以直接放到结果上，因此左括号不用判断其他的
	if left > 0 {
		recursionGenerate(res, tmp+"(", left-1, right)
  }
  // 而有括号需要跟左括号匹配，所以有括号遍历的时候 必须已经有左括号被放到了结果中
  // 所以需要判断一下 right > left
	if right > left {
		recursionGenerate(res, tmp+")", left, right-1)
	}
}

public List<String> generateParenthesis(int n) {
    List<String> res = new ArrayList<>();
    recursion(res, n, n, "");
    return res;
}

public void recursion(List<String> res, int left, int right, String tmp) {
    if (left == 0 && right == 0) {
        res.add(tmp);
        return;
    }

    if (left > 0) {
        recursion(res, left - 1, right, tmp + "(");
    }
    if (right > left) {
        recursion(res, left, right - 1, tmp + ")");
    }
}

正则表达式匹配

这道题可以用递归的思想去做，也可以采用 dp 的方法。实际上递归就是从上向下的 dp

func isMatch(s string, p string) bool {
	return recursionIsMatch(s, p, 0, 0)
}

func recursionIsMatch(s, p string, sIndex, pIndex int) bool {
	// 完全匹配
	if sIndex == len(s) && pIndex == len(p) {
		return true
	}
	// 越界 pattern 匹配完了一定有问题
	if pIndex == len(p) && sIndex != len(s) {
		return false
	}

	if pIndex < len(p)-1 && p[pIndex+1] == '*' {
		// 匹配
		if pIndex < len(p) && sIndex < len(s) && (p[pIndex] == s[sIndex] || p[pIndex] == '.') {
			return recursionIsMatch(s, p, sIndex, pIndex+2) || // 匹配0次 因为 * 代表 0 -> 多次
				recursionIsMatch(s, p, sIndex+1, pIndex+2) || // 匹配1次
				recursionIsMatch(s, p, sIndex+1, pIndex) // 匹配多次
		} else {
			// 如果不匹配 则跳过
			return recursionIsMatch(s, p, sIndex, pIndex+2)
		}
	}
	// 现在的字符是匹配的
	if pIndex < len(p) && sIndex < len(s) && (p[pIndex] == s[sIndex] || p[pIndex] == '.') {
		return recursionIsMatch(s, p, sIndex+1, pIndex+1)
	}
	return false
}

public boolean isMatch(String s, String p) {
    return recursion(s, p, 0, 0);
}

public boolean recursion(String s, String p, int sIndex, int pIndex) {
    if (pIndex == p.length() && sIndex != s.length()) {
        return false;
    }

    if (sIndex == s.length() && pIndex == p.length()) {
        return true;
    }

    if (pIndex < p.length() - 1 && p.charAt(pIndex + 1) == '*') {
        if (sIndex < s.length() && (p.charAt(pIndex) == '.' || p.charAt(pIndex) == s.charAt(sIndex))) {
            return recursion(s, p, sIndex, pIndex + 2) || // 匹配0次
                    recursion(s, p, sIndex + 1, pIndex + 2) || // 匹配1次
                    recursion(s, p, sIndex + 1, pIndex); // 匹配多次
        } else {
            return recursion(s, p, sIndex, pIndex + 2);
        }
    }
    if (sIndex < s.length() && pIndex < p.length() && (p.charAt(pIndex) == '.' || p.charAt(pIndex) == s.charAt(sIndex))) {
        return recursion(s, p, sIndex + 1, pIndex + 1);
    }
    return false;
}

数据结构

栈和队列

队列-滑动窗口的最大值

最大 queue 的队列

type MaxQueue struct {
	stack1 MaxStack
	stack2 MaxStack
}

func (queue *MaxQueue) Push(val int) {
	queue.stack1.Push(val)
}

func (queue *MaxQueue) shift() int {
	if queue.stack2.Len() == 0 {
		for queue.stack1.Len() > 0 {
			queue.stack2.Push(queue.stack1.Pop())
		}
	}
	return queue.stack2.Pop()
}

func (queue *MaxQueue) Max() int {
	if queue.stack1.Len() == 0 {
		return queue.stack2.Max()
	} else if queue.stack2.Len() == 0 {
		return queue.stack1.Max()
	}
	return max(queue.stack2.Max(), queue.stack1.Max())
}

func (queue *MaxQueue) Len() int {
	return queue.stack1.Len() + queue.stack2.Len()
}

type MaxStack struct {
	// 这两个不用 slice 用 list 之类的链表 可能会快一点儿
	data  []int
	maxes []int
}

func (ms *MaxStack) Push(val int) {
	ms.data = append(ms.data, val)
	if len(ms.maxes) > 0 {
		ms.maxes = append(ms.maxes, max(ms.maxes[len(ms.maxes)-1], val))
	} else {
		ms.maxes = append(ms.maxes, val)
	}
}

func (ms *MaxStack) Pop() int {
	res := ms.data[len(ms.data)-1]
	ms.data = ms.data[:len(ms.data)-1]
	ms.maxes = ms.maxes[:len(ms.maxes)-1]
	return res
}

func (ms *MaxStack) Max() int {
	return ms.maxes[len(ms.maxes)-1]
}

func (ms *MaxStack) Len() int {
	return len(ms.data)
}

使用代码

func maxSlidingWindow(nums []int, k int) []int {
	queue := MaxQueue{
		stack1: MaxStack{},
		stack2: MaxStack{},
	}

	for i := 0; i < k; i++ {
		queue.Push(nums[i])
	}
	res := make([]int, 0)
	for i := k; i < len(nums); i++ {
		res = append(res, queue.Max())
		queue.shift()
		queue.Push(nums[i])
	}
	res = append(res, queue.Max())
	return res
}

栈-计算器

中值表达式转波兰表达式（实际上是）

链表

删除倒数的第 N 个节点

func removeNthFromEnd(head *ListNode, n int) *ListNode {
	// 因为可能删除头结点 所有加了一个
	newHead := new(ListNode)
	newHead.Next = head
	// fast 是先走的一个节点 pre 是后走的
	pre, fast := newHead, head
	for n > 0 {
		// 有问题 数量不够
		if fast == nil {
			return nil
		}
		fast = fast.Next
		n--
	}
	// 两个指针开始走
	for fast != nil {
		fast = fast.Next
		pre = pre.Next
	}

	pre.Next = pre.Next.Next
	return newHead.Next
}

合并 k 个已经排序的链表

类似归并排序

package classic

// mergeKLists 合并k个已经按照升序排列的数组
func mergeKLists(lists []*ListNode) *ListNode {
	return merge(lists,0, len(lists) - 1)
}

func merge(lists []*ListNode, start, end int) *ListNode {
	if start > end {
		return nil
	}
	if start == end {
		return lists[start]
	}
	mid := (start + end) / 2
	left, right := merge(lists, start, mid), merge(lists, mid + 1, end)
	return mergeTwoList(left, right)
}

func mergeTwoList(list1 *ListNode, list2 *ListNode) *ListNode {
	res := new(ListNode)
	rem := res

	for list1 != nil && list2 != nil {
		if list1.Val > list2.Val {
			res.Next = list2
			list2 = list2.Next
		} else {
			res.Next = list1
			list1 = list1.Next
		}
		res = res.Next
	}
	if list1 != nil {
		res.Next = list1
	}
	if list2 != nil {
		res.Next = list2
	}
	return rem.Next
}

翻转链表一系列

反转链表

最简单的反转链表的思路肯定是直接用一个 stack，FILO 的机制来反转，而不采用额外的空间可以用一下的方法

func reverseList(head *ListNode) *ListNode {
    // 反转后的头节点
	var pre *ListNode = nil

	for head != nil {
        // 用一个 局部变量 来保存下一个节点
        next := head.Next

        // 反转当前遍历的 head 节点，指向已经反转完毕的头结点
		head.Next = pre
        pre = head
        // 重新设置 head 头
		head = next
	}
	return pre
}

反转链表 II

反转链表 II 是反转链表下表从 m -> n 的一个链表，实际上采用上述的反转的操作，即可反转 m -> n 之间的节点

// 主函数
func reverseBetween(head *ListNode, m int, n int) *ListNode {
    // 添加一个新的头结点，保障原来的头结点被反转时的结果
	newHead := new(ListNode)
	newHead.Next = head
    cp := newHead
    // 分别保存需要反转的节点之前的一个节点以及最后需要反转的一个节点
	var preStartNode, endNode *ListNode = nil, nil
	for i := 0; cp != nil; cp, i = cp.Next, i + 1 {
		if i == m - 1 {
			preStartNode = cp
		}
		if i == n {
			endNode = cp
		}
    }
    // 保存反转完毕后的链表需要连接到的下一个节点
	afterEndNode := endNode.Next
	reverseHead, reverseEnd := reverseBetweenNodes(preStartNode.Next, afterEndNode)
	preStartNode.Next = reverseHead
	reverseEnd.Next = afterEndNode

	return newHead.Next
}

// reverseBetweenNodes reverse两个node之间的链表
// 其中 startNode 为开始翻转的节点 endNodeNext 为结束翻转的节点的后一个节点
func reverseBetweenNodes(startNode, endNodeNext *ListNode) (*ListNode, *ListNode) {
	var newHead *ListNode = nil
	newEndNode := startNode
	for startNode != endNode {
		next := startNode.Next
		startNode.Next = newHead
		newHead = startNode
		startNode = next
	}
	return newHead, newEndNode
}

reverse K group

reverse K group 的更进一步，在上面一题的基础上，每 K 个节点反转一次

// reverseKGroup k个一组翻转
func reverseKGroup(head *ListNode, k int) *ListNode {
	newHead := new(ListNode)
	newHead.Next = head

	var preStartNode, endNode *ListNode = newHead, nil
	counter := 0
	mov := newHead

	for mov != nil {
		if counter == k {
			endNode = mov
            afterEnd := endNode.Next
            // 调用二题中所述的函数进行反转
			reverseHead, reverseEnd := reverseBetweenNodes(preStartNode.Next, endNode.Next)
			preStartNode.Next = reverseHead
			reverseEnd.Next = afterEnd
            // 因为反转之后要重新记录 preStartNode
            counter = 0
            // 反转之后的需要再次反转的头是上次反转的尾结点
			preStartNode = reverseEnd
			// 重新定位移标
			mov = reverseEnd
		}
		mov = mov.Next
		counter++
	}

	return newHead.Next
}

// reverseBetweenNodes reverse两个node之间的链表
// 其中 startNode 为开始翻转的节点 endNodeNext 为结束翻转的节点的后一个节点
func reverseBetweenNodes(startNode, endNodeNext *ListNode) (*ListNode, *ListNode) {
	var newHead *ListNode = nil
	newEndNode := startNode
	for startNode != endNodeNext {
		next := startNode.Next
		startNode.Next = newHead
		newHead = startNode
		startNode = next
	}
	return newHead, newEndNode
}

树

树的遍历

中序遍历

func inorderTraversal(root *TreeNode) []int {
	res := make([]int, 0)

	stack := list.New()

	for root != nil || stack.Len() != 0 {
		for root != nil {
			stack.PushBack(root)
			root = root.Left
		}
		if stack.Len() > 0 {
			root = stack.Remove(stack.Back()).(*TreeNode)
			res = append(res, root.Val)
			root = root.Right
		}
	}
	return res
}

前序遍历

package classic

import "container/list"

func preorderTraversal(root *TreeNode) []int {
	res := make([]int, 0)

	stack := list.New()

	for root != nil || stack.Len() > 0 {
		for root != nil {
			res = append(res, root.Val)
			stack.PushBack(root)
			root = root.Left
		}
		if stack.Len() > 0 {
			root = stack.Remove(stack.Back()).(*TreeNode)
			root = root.Right
		}
	}
	return res
}

后序遍历

func postorderTraversal(root *TreeNode) []int {
	res := make([]int, 0)

	stack := list.New()
	// 标识这个node是不是第二次访问
	stackForFlag := list.New()
	for root != nil || stack.Len() > 0 {
		for root != nil {
			stack.PushBack(root)
			stackForFlag.PushBack(false)
			root = root.Left
		}

		if stack.Len() > 0 {
			root = stack.Remove(stack.Back()).(*TreeNode)
			flag := stackForFlag.Remove(stackForFlag.Back()).(bool)

			// 说明是第二次访问 这个时候要访问父亲节点
			if flag {
				res = append(res, root.Val)
				root = nil
			} else {
				// 第一次访问
				stack.PushBack(root)
				stackForFlag.PushBack(true)
				root = root.Right
			}
		}
	}
	return res
}

层次遍历

1. 普通层次遍历

func levelOrder(root *TreeNode) [][]int {
	res := make([][]int, 0)
    if root == nil {
		return res
	}
	tmp := make([]int, 0)
	queue := list.New()
	queue.PushBack(root)
	queue.PushBack(nil)
	for queue.Len() > 0 {
		node := queue.Remove(queue.Front())
		if node == nil {
			cp := make([]int, len(tmp))
			copy(cp, tmp)
			res = append(res, cp)
            if queue.Len() == 0 {
				break
			}
			queue.PushBack(nil)
			tmp = make([]int, 0)
			continue
		}
		top := node.(*TreeNode)
		if top.Left != nil {
			queue.PushBack(top.Left)
		}
		if top.Right != nil {
			queue.PushBack(top.Right)
		}
		tmp = append(tmp, top.Val)
	}
	return res
}

2. zigzag 的层次遍历

package classic

import "container/list"

func zigzagLevelOrder(root *TreeNode) [][]int {

	res := make([][]int, 0)
	if root == nil {
		return res
	}
	isLeft := true
	tmp := make([]int, 0)
	queue := list.New()

	queue.PushBack(root)
	queue.PushBack(nil)

	for queue.Len() > 0 {
		top := queue.Remove(queue.Front())
		if top == nil {
			cp := make([]int, len(tmp))
			copy(cp, tmp)
			res = append(res, cp)
			if queue.Len() == 0 {
				break
			}
			isLeft = !isLeft
			tmp = make([]int, 0)
			queue.PushBack(nil)
			continue
		}
		node := top.(*TreeNode)
		if node.Left != nil {
			queue.PushBack(node.Left)
		}
		if node.Right != nil {
			queue.PushBack(node.Right)
		}
		// 这个地方可以这样加入 就不用再 top == nil 中重新反转数组
		if isLeft {
			tmp = append(tmp, node.Val)
		} else {
			tmp = append([]int{node.Val}, tmp...)
		}
	}
	return res
}

前缀树

实现用字符串的前缀来索引的结构树

// Trie 之间通过 字符 关联 上一个 trie 会通过字符作为边连接下一个节点
type Trie struct {
	data  []*Trie // 存储索引结构的数 因为只包含 a-z 的字母 索引直接数组即可 不然用 map 会更好
	isEnd bool    // 是否结束节点
}

/** Initialize your data structure here. */
func Constructor() Trie {
	return Trie{
		data:  make([]*Trie, 26),
		isEnd: false,
	}
}

/** Inserts a word into the trie. */
func (this *Trie) Insert(word string) {
	tmp := this
	for _, char := range word {
		if tmp.data[char-'a'] == nil {
			tmp.data[char-'a'] = &Trie{
				data:  make([]*Trie, 26),
				isEnd: false,
			}
		}
		tmp = tmp.data[char-'a']
	}
	tmp.isEnd = true
}

/** Returns if the word is in the trie. */
func (this *Trie) Search(word string) bool {
	tmp := this
	for _, char := range word {
		if tmp.data[char-'a'] == nil {
			return false
		}
		tmp = tmp.data[char-'a']
	}
	return tmp.isEnd
}

/** Returns if there is any word in the trie that starts with the given prefix. */
func (this *Trie) StartsWith(prefix string) bool {
	tmp := this
	for _, char := range prefix {
		if tmp.data[char-'a'] == nil {
			return false
		}
		tmp = tmp.data[char-'a']
	}
	return true
}

图

并查集的数据结构

并查集，表示的是一个树形的结构

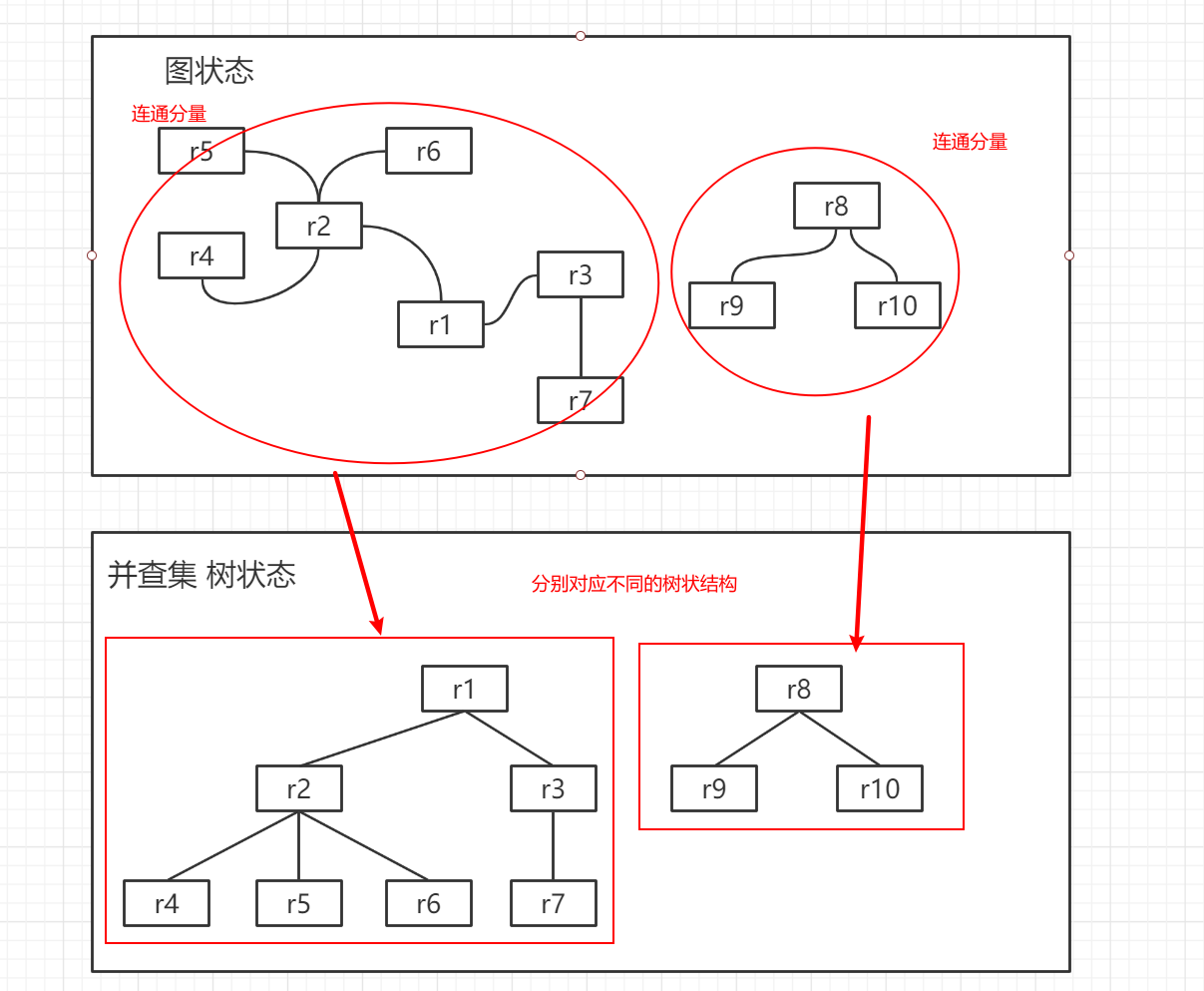
如图所示，针对图的一个极大连通分量，会形成一个对应的树结构（并查集只关注一个连通分量有多少连接点，不关注内部的其他的细节）

所以针对查找连通分量有哪些，以及连同量间的关系有作用

并查集存储数据的结构

type Union struct {
	parents []int // 存储树的数据结构 parents[i] 表示连接到该节点的父节点的索引 如果不能用 int 来表示 可以考虑 map 类的数据结构
}

并查集的操作

• union (联合，关联两个点)
• find (查找，找到当前点的最终的父节点)

所以，实际上 如果 r1 r2 之间有连接线的话，要关联 r1 r2 的操作就是。

• 就是通过 find 找到分别的根节点 r1Root r2Root
• 在通过 union 方法关联两个根节点，实际上就是将 r2Root 作为一个子节点，挂载到 r1Root 下

所以整体的数据结构为

type unionFind struct {
	Parents []int
	Count   int     // 表示连通分量的多少
}

func NewUnionFind(size int) *unionFind {
	res := &unionFind{
		Parents: make([]int, size),
		Count:   size,
	}
	// 初始化并查集中的每个元素的父节点都是自己
	for i := 0; i < size; i++ {
		res.Parents[i] = i
	}
	return res
}

func (u *unionFind) union(i, j int) {
	iRoot := u.find(i)
	jRoot := u.find(j)
	if iRoot != jRoot {
		u.Parents[jRoot] = iRoot
		// 每次连接一个之后 最大连通分量就要 --
		u.Count--
	}
}

func (u *unionFind) find(i int) int {
	if u.Parents[i] == i {
		return i
	}
	return u.find(u.Parents[i])
}

func (u *unionFind) GetCount() int {
	return u.Count
}

执行交换操作后的最小汉明距离

这道题实际上是找连通分量，对比两个数组中相应的连通区域不等的部分，所以可以用无向图连通分量 dfs or 并查集 得到连通分量后进行处理。

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;

public class MinimumHammingDistance_1722 {

    public void union(int[] union, int i, int j) {
        int x = getParent(union, i);
        int y = getParent(union, j);
        if (x != y) {
            union[y] = x;
        }
    }

    public int getParent(int[] union, int i) {
        if (union[i] == -1) return i;
        return getParent(union, union[i]);
    }

    public void changeUnion(int[] union) {
        boolean[] memo = new boolean[union.length];

        for (int i = 0; i < union.length; i++) {
            if (!memo[i]) {
                recursion(union, memo, i);
            }
        }
    }

    // 更该 union 到root
    public int recursion(int[] union, boolean[] memo, int i) {
        if (memo[i]) return union[i];
        memo[i] = true;
        if (union[i] == -1 || union[i] == i) {
            union[i] = i;
            return i;
        }
        int root = recursion(union, memo, union[i]);
        union[i] = root;
        return root;
    }

    // 连通图问题 在连通分量里面找到不等的数字
    // 无向图的连通分量
    // 可以使用 dfs 得到无向图的连通分量 or 使用 union 的算法得到连通分量
    // 但是 union 算法如果直接在算法执行图中去更改所有的 root 值 会慢一点儿 所以在执行完毕后去更改
    public int minimumHammingDistance(int[] source, int[] target, int[][] allowedSwaps) {
        int[] union = new int[source.length];
        Arrays.fill(union, -1);

        for (int[] allowSwap : allowedSwaps) {
            union(union, allowSwap[0], allowSwap[1]);
        }

        // 修改连通分量标识 到根节点
        changeUnion(union);
        // 现在每个中对应的都是一个连通分量的根节点的下标，那么就需要知道 一个连通分量里面有多少个不等的

        // 保存root中的数字每个出现了几次
        Map<Integer, Map<Integer, Integer>> sMap = new HashMap<>();
        for (int i = 0; i < union.length; i++) {
            int root = union[i];
            if (!sMap.containsKey(root)) sMap.put(root, new HashMap<>());
            Map<Integer, Integer> tmp = sMap.get(root);
            tmp.put(source[i], tmp.getOrDefault(source[i], 0) + 1);
        }

        int res = 0;
        for (int i = 0; i < union.length; i++) {
            int root = union[i];
            Map<Integer, Integer> tmp = sMap.get(root);
            if (!tmp.containsKey(target[i]) || tmp.get(target[i]) == 0) {
                res++;
            } else {
                tmp.put(target[i], tmp.get(target[i]) - 1);
            }
        }
        return res;
    }

    public static void main(String[] args) {
        System.out.println(new MinimumHammingDistance_1722().minimumHammingDistance(new int[]{49, 21, 79, 79, 6, 67, 78, 9, 91, 39, 49, 32, 53, 29, 97, 50, 82, 55, 13, 83, 63, 99, 41, 6, 51, 46, 31, 26, 58, 18, 32, 51, 44, 66, 40, 35, 96, 20, 35, 43, 64, 96, 99, 76, 11, 35, 86, 96, 10, 19, 70, 29, 19, 47}, new int[]{33, 22, 32, 71, 66, 90, 78, 67, 74, 76, 84, 32, 25, 100, 57, 7, 90, 95, 33, 79, 54, 99, 42, 6, 32, 55, 31, 14, 58, 67, 48, 59, 7, 50, 5, 22, 11, 97, 94, 14, 53, 75, 3, 9, 82, 74, 86, 27, 21, 77, 70, 29, 65, 15}, new int[][]{{40, 41}, {41, 35}, {18, 19}, {9, 51}, {48, 2}, {45, 13}, {27, 45}, {16, 22}, {23, 25}, {2, 6}, {5, 11}, {37, 38}, {22, 48}, {13, 48}, {51, 37}, {24, 19}, {2, 32}, {38, 23}, {33, 34}, {37, 44}, {31, 8}, {4, 26}, {34, 35}, {37, 28}, {48, 34}, {27, 0}, {23, 37}, {17, 29}, {38, 7}, {37, 31}, {34, 42}, {26, 20}, {22, 45}, {26, 29}, {40, 42}, {48, 30}, {46, 49}, {12, 52}, {49, 28}, {39, 14}, {23, 34}, {6, 30}, {18, 12}, {52, 49}, {21, 18}, {11, 4}, {2, 7}, {4, 17}, {19, 27}, {33, 5}, {44, 28}, {38, 9}, {34, 7}, {7, 47}, {37, 13}, {51, 12}, {42, 53}, {42, 21}, {18, 9}, {21, 39}, {4, 33}, {29, 39}, {47, 41}, {25, 13}, {50, 0}, {21, 48}, {32, 27}, {33, 53}, {39, 5}, {12, 25}, {52, 6}, {17, 44}, {16, 52}, {0, 34}, {14, 29}, {0, 19}, {13, 7}, {29, 21}, {9, 22}, {28, 45}, {1, 29}, {37, 17}, {38, 36}, {4, 23}, {38, 21}, {35, 5}, {2, 16}, {34, 30}, {37, 16}, {40, 53}, {51, 47}, {20, 32}, {7, 9}, {12, 15}, {26, 0}, {14, 44}, {53, 11}, {48, 17}}));
    }
}

连通网络的操作次数

题目所述，给定一个图，找到将其所有最大连通分量连通所需更改的最少的边的数量为多少。

图的所有最小连通为一个树，即需要 n 个节点有 n - 1 条边。

所以题目其实是要找到这个图里面有多少独立的连通分量，然后判断其是否可以连接

• 第一种思路就是直接 dfs 遍历，找到所有的连通分量。首先判断边的数量是否足够 n - 1 这个时候，如果有多个连通分量，说明某个连通分量一定有多的边，随意选取其中的边即可

package classic

// makeConnected 方法查看
func makeConnected(n int, connections [][]int) int {
	// 最短的话肯定是形成一棵树 才能联通所有
	// 所以 边 至少要达到 n - 1 的数量
	// 这个时候不能连通
	if len(connections) < n-1 {
		return -1
	}
	// map 的邻接表表示
	cMap := make(map[int][]int)
	for _, connection := range connections {
		if _, ok := cMap[connection[0]]; !ok {
			cMap[connection[0]] = make([]int, 0)
		}
		cMap[connection[0]] = append(cMap[connection[0]], connection[1])

		if _, ok := cMap[connection[1]]; !ok {
			cMap[connection[1]] = make([]int, 0)
		}
		cMap[connection[1]] = append(cMap[connection[1]], connection[0])
	}

	// 到这里的时候 由于边的数量够 所以一定是可以连通的
	// 这个时候 只需要知道有 m 块是不相连的 然后就知道需要连接的次数就为 m - 1
	memo := make([]bool, n)
	res := 0
	for i := 0; i < n; i++ {
		if !memo[i] {
			res++
			dfs(memo, cMap, i)
		}
	}
	return res - 1
}

func dfs(memo []bool, cMap map[int][]int, start int) {
	memo[start] = true
	for _, next := range cMap[start] {
		if !memo[next] {
			dfs(memo, cMap, next)
		}
	}
}

• 并查集，找到每个群组的数据的一个代表点

// findRoot 找到根节点
func findRoot(parents []int, index int) int {
	if parents[index] == -1 {
		return index
	}
	return findRoot(parents, parents[index])
}

// makeConnected 并查集
func makeConnected(n int, connections [][]int) int {
	if len(connections) < n - 1 {
		return -1
	}

	// 并查集的 parents 数组，标识 当前索引的 节点的父节点的索引是谁
	// 相同的数最后均能找到同样的父节点
	parents := make([]int, n)
	// 初始化所有的为 -1
	for i := 0; i < n; i++ {
		parents[i] = -1
	}

	// 执行 union 的操作
	for _, connection := range connections {
		sRoot := findRoot(parents, connection[0])
		eRoot := findRoot(parents, connection[1])

		// 两个点上有连接线 但是现在还没有连接起来
		// 让其根节点相连
		if sRoot != eRoot {
			// 将 e 节点连接到 s 上
			parents[eRoot] = sRoot
		}
	}
	// 剩下的还是 -1 的就一定是整个群里面的代表节点
	res := 0
	for _, val := range parents {
		if val == -1 {
			res++
		}
	}
	return res - 1
}

由斜杠划分区域

采用并查集，但是这道题有特殊的地方。

题目中所示，针对一个方格有 / 和 \ 两种，如下

----    ----
|\ |    | /|
| \|    |/ |
----    ----

总之，针对一个 方格 ，可以把他看成四个部分

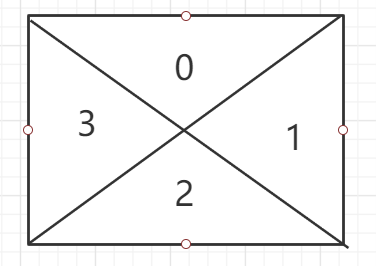
那么，也就是说，

• 如果当前 char == ‘ ‘ 表示 0 1 2 3 都是联通的
• 如果 char == ‘\‘ 表示 01 23 分别连通
• char == ‘/‘ 表示 03 12 分别连通

内部的连通完毕后，

• 还可以知道 1 一定跟下一个 3 连通
• 2 一定跟下一行的 0 连通

// regionsBySlashes 通过斜杠划分
func regionsBySlashes(grid []string) int {
	// n * n 的矩阵的长度
	length := len(grid)
	// 为了使用 并查集 将一个1*1 的正方形，即 一个 grid[i] 标识的区域分成 四个地方
	// 然后再根据 / \\ 两个符号的位置进行合并 最后看有几个节点
	unionSize := 4 * length * length
	u := NewUnionFind(unionSize)

	for i, str := range grid {
		for j, char := range str {
			// 0 号位置
			uIndex := 4 * (i*length + j)

			// 同一个单元格里面的连接起来
			switch char {
			// 0 1 2 3 都要连接起来
			case ' ':
				u.union(uIndex, uIndex + 1)
				u.union(uIndex + 1, uIndex + 2)
				u.union(uIndex + 2, uIndex + 3)
			case '\\':
				// 反斜杠的话 01 23 分别连接
				u.union(uIndex, uIndex + 1)
				u.union(uIndex + 2, uIndex + 3)
			case '/':
				// 斜杠的话 03 12 分贝连接
				u.union(uIndex, uIndex + 3)
				u.union(uIndex + 1, uIndex + 2)
			}
			// 单元格外面的连接起来
			// 不管是 \\ 还是 / 这个区域的1一定可以和右边下一个区域( j+ 1)的 3 连接
			// 这个区域的 2 一定可以和下边(i + 1)下一个区域的 0 连接
			if j + 1 < length {
				u.union(uIndex+1, 4*(i*length+j+1)+3)
			}
			if i + 1 < length {
				u.union(uIndex+2, 4*((i+1)*length+j))
			}
		}
	}

	return u.GetCount()
}

水位上升的泳池中游泳

这道题没想明白最开始，肯定是明白要知道到什么时候 [0,0] 跟 [n - 1, n - 1] 的右下角相连

相连的判断可以通过并查集实现

那么就要解决几个问题：

• 怎么遍历
• 并查集连接的条件是什么
• 怎么把二维数组的位置抽象到一维

从以下几个方面入手

• 题目中所述 grid 中的数值从 [0, nn-1] 的唯一数值，也就是说每个格子的高度都是独立的，因此只需要遍历高度，在遍历高度中如果 [0, nn-1] 相连，即完成连接
• 由于题目中 当遍历的位置达到一个高度的时候，他可以直接和上下左右上的相连，也就是说遍历到高度更高的地方能够直接比高度更低的地方连接
• 而题目中的 grid 的棋盘的二维数组可以通过简单的 n*x+y 抽象到一维

package classic

func union(parents []int, i, j int) {
	iRoot, jRoot := findRootOfParents(parents, i), findRootOfParents(parents, j)
	if iRoot != jRoot {
		parents[jRoot] = iRoot
	}
}

func findRootOfParents(parents []int, i int) int {
	if parents[i] == i {
		return i
	}
	return findRootOfParents(parents, parents[i])
}

func isConnectedParents(parents []int, i, j int) bool {
	return findRootOfParents(parents, i) == findRootOfParents(parents, j)
}

var (
	// 表示上下左右四个方向
	DIRECTIONS = [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}
)

func swimInWater(grid [][]int) int {
	if grid == nil {
		return -1
	}
	n := len(grid)

	index := make([]int, n*n)

	for i := 0; i < n; i++ {
		for j := 0; j < n; j++ {
			// 因为题目中所述，grid 里面的数值从 0 -> n * n - 1
			// 所以让高度作为下标索引 方便下面遍历
			index[grid[i][j]] = n*i + j
		}
	}
	// grid 的二位数组 可以转为 n * i + j 的一维坐标
	parents := make([]int, n*n)
	for i := 0; i < n*n; i++ {
		parents[i] = i
	}

	for i := 0; i < n*n; i++ {
		x, y := index[i]/n, index[i]%n
		for _, direction := range DIRECTIONS {
			newX, newY := x+direction[0], y+direction[1]
			// 因为这个是从高度相距只有1的地方开始的 所以可以直接关联
			// 这样当 0 n - 1 连接到一起的时候 说明已经达到的最小的高度
			// 只有新的节点的高度 小于 当前的高度 才是可以游过去的！！！
			if !(newX < 0 || newX >= n || newY < 0 || newY >= n) && grid[newX][newY] <= i {
				// index 的索引用在这个地方
				union(parents, index[i], newX*n+newY)
			}

			if isConnectedParents(parents, 0, n*n-1) {
				return i
			}
		}
	}
	return -1
}

拓扑排序

• 逆后续排列
• 遍历出度为 0 的点

课程表

这道题本质上就是拓扑排序

简单的做法就是用 dfs 去判断是否成环

func canFinish(numCourses int, prerequisites [][]int) bool {
	// 有向图
	mapOfCourses := make([][]int, numCourses)
	for i := 0; i < numCourses; i++ {
		mapOfCourses[i] = make([]int, 0)
	}
	for _, prerequisite := range prerequisites {
		mapOfCourses[prerequisite[1]] = append(mapOfCourses[prerequisite[1]], prerequisite[0])
	}
	// 保存已经访问过的节点 这样可以避免重复访问
	totalMemo := make([]bool, numCourses)
	for i := 0; i < numCourses; i++ {
		if !dfsCanFinish(mapOfCourses, make([]bool, numCourses), totalMemo, i) {
			return false
		}
	}
	return true
}

// 通过 dfs 的方法判断是否成环
// 用 memo 来记录一次循环中访问的节点
func dfsCanFinish(mapOfCourses [][]int, memo, totalMemo []bool, start int) bool {
	if totalMemo[start] {
		return true
	}
	totalMemo[start] = true
	memo[start] = true
	for _, adj := range mapOfCourses[start] {
		if !memo[adj] {
			// 截断 有环直接返回
			if !dfsCanFinish(mapOfCourses, memo, totalMemo, adj) {
				return false
			}
		} else {
			// 这个地方就是找到了环
			return false
		}
	}
	memo[start] = false
	return true
}

拓扑排序 遍历入度为 0 的点

func canFinish(numCourses int, prerequisites [][]int) bool {

	// 入度为 0 的点为起点
	inDegree := make([]int, numCourses)
	for _, prerequisite := range prerequisites {
		// 让有向图的接受线的一端 入度++
		inDegree[prerequisite[0]]++
	}

	// 保存入度为 0 的点
	inDegreeEqualZero := list.New()
	for i, in := range inDegree {
		if in == 0 {
			inDegreeEqualZero.PushBack(i)
		}
	}

	// 遍历入度为 0 的点
	// 每次删除一条边 判断下一个点 是否入度为0 入度为 0 加入到 map 中 不停的遍历 直到没有点
	for inDegreeEqualZero.Len() > 0 {
		node := inDegreeEqualZero.Remove(inDegreeEqualZero.Front()).(int)
		for _, prerequisite := range prerequisites {
			if node == prerequisite[1] {
				inDegree[prerequisite[0]]--
				if inDegree[prerequisite[0]] == 0 {
					inDegreeEqualZero.PushBack(prerequisite[0])
				}
			}
		}
	}
	for i := 0; i < numCourses; i++ {
		// 这个地方说明还有点相连，因此是无法完成的
		if inDegree[i] != 0 {
			return false
		}
	}
	return true
}

最短路径

地图分析

找到多源最短路，改造了一下 dijkstra 算法

public int maxDistance(int[][] grid) {
		// 考虑使用 dijkstra 算法
		// dijkstra 算法是找单源最短路经的
		// 因此在这儿要改造一下
		// 虚拟出一个超级节点 连接所有的起始节点 那样就可以找出从这个超级节点到 另外一个集合的最短距离

		int n = grid.length;
		int[][] dst = new int[n][n];
		// 无向图 为了防止重复访问 需要 memo
		boolean[][] memo = new boolean[n][n];

		PriorityQueue<Node> pq = new PriorityQueue<>();
		for (int i = 0; i < n; i++) {
				for (int j = 0; j < n; j++) {
						dst[i][j] = Integer.MAX_VALUE;
						// 连接到超级节点的 dst 为 0
						// 从 岸开始遍历 那么 岸到任意一个海的最短距离就会保存到 海节点上
						if (grid[i][j] == 1) {
								dst[i][j] = 0;
								pq.add(new Node(i, j, 0));
						}
				}
		}
		// 这样就可以吧时间复杂度降下来
		while (!pq.isEmpty()) {
				Node top = pq.poll();
				memo[top.x][top.y] = true;
				for (int[] direction : directions) {
						int newX = top.x + direction[0], newY = top.y + direction[1];
						// 越界
						if (newX >= n || newX < 0 || newY >= n || newY < 0) continue;
						if (memo[newX][newY]) continue;
						// relax
						if (dst[newX][newY] > dst[top.x][top.y] + 1) {
								dst[newX][newY] = dst[top.x][top.y] + 1;
								// 更新 pq 里面的最短距离
								pq.removeIf((node) -> node.x == newX && node.y == newY);
								pq.add(new Node(newX, newY, dst[newX][newY]));
						}
				}
		}
		int res = -1;
		for (int i = 0; i < n; i++) {
				for (int j = 0; j < n; j++) {
						// 因为结果保存在 海洋单元格内
						if (grid[i][j] == 0) res = Math.max(res, dst[i][j]);
				}
		}
		return res == Integer.MAX_VALUE ? -1 : res;
}

private static class Node implements Comparable<Node> {
		int x, y;

		int dst;

		public Node(int x, int y) {
				this.x = x;
				this.y = y;
				// 还没有找到
				this.dst = Integer.MAX_VALUE;
		}

		public Node(int x, int y, int dst) {
				this.x = x;
				this.y = y;
				this.dst = dst;
		}

		@Override
		public int compareTo(Node o) {
				return this.dst - o.dst;
		}
}

private static int[][] directions = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

1786. 从第一个节点出发到最后一个节点的受限路径数

说实话 我是看不懂受限路径到底是什么意思，所以看了下他们的思路，自己实现了一下。现在贴上原题

现有一个加权无向连通图。给你一个正整数 n ，表示图中有 n 个节点，并按从 1 到 n 给节点编号；另给你一个数组 edges ，其中每个 edges[i] = [ui, vi, weighti] 表示存在一条位于节点 ui 和 vi 之间的边，这条边的权重为 weighti 。


从节点 start 出发到节点 end 的路径是一个形如 [z0, z1, z2, …, zk] 的节点序列，满足 z0 = start 、zk = end 且在所有符合 0 <= i <= k-1 的节点 zi 和 zi+1 之间存在一条边。


路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。受限路径 为满足 distanceToLastNode(zi) > distanceToLastNode(zi+1) 的一条路径，其中 0 <= i <= k-1 。


返回从节点 1 出发到节点 n 的 受限路径数 。由于数字可能很大，请返回对 109 + 7 取余 的结果。

• 参考的解法

• 模仿的解法

超时，怀疑是 构建图 花费太多时间

import microsoft.PlusOne;

import java.util.*;

public class CountRestrictedPaths_1786 {

    private static class Edge {
        int from, to;
        int weight;

        public Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }

        public int getOther(int node) {
            if (node == from) return to;
            return from;
        }
    }

    private static class Map {
        List<List<Edge>> map;
        public int capacity;

        public Map(int capacity) {
            this.capacity = capacity;
            this.map = new ArrayList<>();
            for (int i = 0; i < this.capacity; i++) {
                this.map.add(new ArrayList<>());
            }
        }

        public void addEdge(int from, int to, int weight) {
            Edge e = new Edge(from, to, weight);
            this.map.get(from).add(e);
            this.map.get(to).add(e);
        }

        public List<Edge> adj(int node) {
            return this.map.get(node);
        }
    }

    private static class Pair implements Comparable<Pair> {
        int node;
        int weight;

        public Pair(int node, int weight) {
            this.node = node;
            this.weight = weight;
        }

        @Override
        public int compareTo(Pair o) {
            return weight - o.weight;
        }
    }

    // 返回 dp 结果
    // 这个题目说的意思是 只要从尾结点开始遍历 并且到下一个点的距离 大于 当前点的距离 就是逆序的
    // 按照题解的描述
    // 这条路径的搜索过程可以看做，从结尾（第 5 个点）出发，逆着走，每次选择一个点（例如 a）之后，
    // 再选择下一个点（例如 b）时就必须满足最短路距离比上一个点（点 a）要远，如果最终能选到起点（第一个点），说明统计出一条有效路径。
    public int[] dijkstra(Map map, int start) {
        int[] dstTo = new int[map.capacity];
        Arrays.fill(dstTo, Integer.MAX_VALUE);
        dstTo[start] = 0;

        PriorityQueue<Pair> queue = new PriorityQueue<>();
        queue.add(new Pair(start, 0));

        // 无向图 防止重复
        boolean[] memo = new boolean[map.capacity];

        while (!queue.isEmpty()) {
            Pair top = queue.poll();
            memo[top.node] = true;
            for (Edge e : map.adj(top.node)) {
                int other = e.getOther(top.node);
                if (!memo[other] && dstTo[other] > dstTo[top.node] + e.weight) {
                    dstTo[other] = dstTo[top.node] + e.weight;
                    queue.removeIf((p) -> p.node == other);
                    queue.add(new Pair(other, dstTo[other]));
                }
            }
        }
        return dstTo;
    }

    public int countRestrictedPaths(int n, int[][] edges) {
        Map map = new Map(n + 1);

        for (int[] edge : edges) {
            map.addEdge(edge[0], edge[1], edge[2]);
        }

        // 返回节点的数据
        int[] dstTo = dijkstra(map, n);

        // 得到了dist数组，可以得到递推关系，dp[u] += dp[v], when v links to v and  dist[u] > dist[v]
        //        因此先算dist小的，才可以算dp，需要dist从小到大排序, 然后依次计算。
        // 保存到某个点 以及对应的 dst 距离
        List<int[]> pairs = new ArrayList<>();
        for (int i = 1; i < dstTo.length; i++) {
            pairs.add(new int[]{i, dstTo[i]});
        }
        pairs.sort(Comparator.comparingInt(a -> a[1]));

        int[] dp = new int[n + 1];
        dp[n] = 1;
        int mod = 1000000007;

        for (int[] p : pairs) {
            int node = p[0], cur = p[1];
            for (Edge adj : map.adj(node)) {
                int other = adj.getOther(node);
                if (cur > dstTo[other]) {
                    dp[node] = (dp[node] + dp[other]) % mod;
                }
            }
        }
        return dp[1];
    }

    public static void main(String[] args) {
        System.out.println(new CountRestrictedPaths_1786().countRestrictedPaths(5, new int[][]{
                {1, 2, 3},
                {1, 3, 3},
                {2, 3, 1},
                {1, 4, 2},
                {5, 2, 2},
                {3, 5, 1},
                {5, 4, 10}
        }));
        System.out.println(new CountRestrictedPaths_1786().countRestrictedPaths(7, new int[][]{
                {1, 3, 1},
                {4, 1, 2},
                {7, 3, 4},
                {2, 5, 3},
                {5, 6, 1},
                {6, 7, 2},
                {7, 5, 3},
                {2, 6, 4}
        }));
    }
}

博弈问题

预测赢家

分别从数组的两端取值，问最后谁获胜。

模拟取值的过程即可

public boolean PredictTheWinner(int[] nums) {
		int[][] memo = new int[nums.length][nums.length];
		for (int[] ints : memo) {
				Arrays.fill(ints, -1);
		}
		return recursionMemo(nums, 0, nums.length - 1, memo) >= 0;
}

public int recursionMemo(int[] nums, int i, int j, int[][] memo) {
		if (i > j) return 0;
		if (i == j) return nums[i];
		if (memo[i][j] != -1) return memo[i][j];
		// 分别选取左边和右边的值进行比较
		int left = nums[i] - recursionMemo(nums, i + 1, j, memo);
		int right = nums[j] - recursionMemo(nums, i, j - 1, memo);
		memo[i][j] = Math.max(left, right);
		return memo[i][j];
}

石子游戏

石子游戏 VII

杂题

递增的三元子序列

• 首先想到嘛，用两个数组分别存储从左到右的最小值和最右到左的最大值，那么如果 nums 中一个数 num 大于这个最小值小于这个最大值，是一定可以的

func increasingTriplet(nums []int) bool {
	if len(nums) == 0 {
		return false
	}
	mins, maxes := make([]int, len(nums)), make([]int, len(nums))
	mins[0] = nums[0]
	for i := 1; i < len(nums); i++ {
		mins[i] = min(mins[i-1], nums[i])
	}

	maxes[len(nums)-1] = nums[len(nums)-1]
	for i := len(nums) - 2; i >= 0; i-- {
		maxes[i] = max(maxes[i+1], nums[i])
	}

	for i, num := range nums {
		if num > mins[i] && num < maxes[i] {
			return true
		}
	}
	return false
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

• 还可以进一步优化

他实际上是找这么一组 3 个数 num1 < num2 < num3

那么如果我在 num3 之前找到了这两个数字 num1 num2 即可

所以用 一个 min mid 来记录之前找到的 num1 num2。

其中 min 保存之前遇到的最小值, mid 保存之前 大于 min 的最小值，那么 如果碰到 同时大于 min、mid 的数 就可以直接返回 true 了。

但是可能遇到这种情况，在访问找到 num3 的时候，min 对应的数字的下标在 mid 之后。

但是考虑这种情况的话，一定有一个小于 mid 的 历史 min 值在 mid 之前，所以其实还是一个完整的三元组。

class Solution {
    public boolean increasingTriplet(int[] nums) {
        if (nums == null || nums.length < 3) return false;
        int min = Integer.MAX_VALUE, mid = Integer.MAX_VALUE;
        for (int num : nums) {
            if (num <= min) {
                min = num;
            } else if (num <= mid) {
                mid = num;
            } else {
                return true;
            }
        }
        return false;
    }
}

二分

袋子里最少数目的球

给你一个整数数组 nums ，其中 nums[i] 表示第 i 个袋子里球的数目。同时给你一个整数 maxOperations 。

你可以进行如下操作至多 maxOperations 次：

选择任意一个袋子，并将袋子里的球分到 2 个新的袋子中，每个袋子里都有 正整数 个球。

比方说，一个袋子里有 5 个球，你可以把它们分到两个新袋子里，分别有 1 个和 4 个球，或者分别有 2 个和 3 个球。

你的开销是单个袋子里球数目的 最大值 ，你想要 最小化 开销。

请你返回进行上述操作后的最小开销。

• bruteforce

直接的做法就是不停的找到数组中最大的数，然后在 maxOperations 的次数限制内进行分隔，找到分隔中最小的数据。

为了 o(1) 的找到最大的数，所以使用的 pq 来保存中间数据

// bruteforce 模拟的方法 通过对递归的方法对最大数进行不停的分隔 得到最后的结果
public int minimumSizeBruteForce(int[] nums, int maxOperations) {
		PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);
		for (int num : nums) {
				pq.add(num);
		}
		return recursion(pq, maxOperations);
}

public int recursion(PriorityQueue<Integer> pq, int operations) {
		assert !pq.isEmpty();
		if (operations == 0) return pq.peek();
		int max = pq.poll();
		int res = Integer.MAX_VALUE;
		for (int i = 1; i <= max / 2; i++) {
				int other = max - i;
				pq.add(i);
				pq.add(other);
				res = Math.min(res, recursion(pq, operations - 1));
				pq.remove(i);
				pq.remove(other);
		}
		pq.add(max);
		return res;
}

• 二分查找

二分查找可以用于查找最小的最大值，最大的最小值等情况。

那么可以以结果作为区间，每次判断这个最小开销是否能够实现，就可以去缩短遍历的范围。

但是需要知道如何找到能否实现这个函数：

• 当用 mid 去规定最小开销的时候，意味着所有大于 mid 的数字都需要被拆分到最小开销中
• 拆分的时候，如 num = 8, mid = 4, 那么只需要拆分一次即可，如 num = 17, mid = 7，那么需要拆分成[7,7,3] 需要拆分两次。所以拆分的代价是 num / mid，在 num % mid == 0 时要减一

// 二分查找 二分的范围是返回的最小结果
// 即最小代价
public int minimumSize(int[] nums, int maxOperations) {
		// nums 中最大的数为 j 的大小
		int i = 1, j = 1000000000;
		int res = 0;
		while (i <= j) {
				int mid = i + (j - i) / 2;
				if (check(nums, mid, maxOperations)) {
						j = mid - 1;
						res = mid;
				} else {
						i = mid + 1;
				}
		}
		return res;
}

// 检查当前遍历到的 mid 的状态 能不能在 maxOperations 的限制下达到
public boolean check(int[] nums, int mid, int maxOperations) {
		int res = 0;
		for (int num : nums) {
				if (num % mid == 0) {
						res += num / mid - 1;
				} else {
						res += num / mid;
				}
		}
		return res <= maxOperations;
}

找出第 k 小的距离对

距离差定义为 数组中 任意一对数之间的差的绝对值

• 因此找到第 K 个最小距离，一个直观的解法就是，遍历所有的差，放入到只有 k 个数的大顶堆中，那么堆顶都是结果。（memory 爆了）

type IntHeap []int

func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IntHeap) Push(x interface{}) {
	// Push and Pop use pointer receivers because they modify the slice's length,
	// not just its contents.
	*h = append(*h, x.(int))
}

func (h *IntHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

// 找到 nums 中第k小一对数之间的最短距离（距离为两数之差）
// heap outOfMemory
func smallestDistancePairWithHeap(nums []int, k int) int {
	hp := &IntHeap{}
	heap.Init(hp)

	for i := 0; i < len(nums); i++ {
		for j := i + 1; j < len(nums); j++ {
			heap.Push(hp, int(math.Abs(float64(nums[i]-nums[j]))))
			if hp.Len() > k {
				heap.Pop(hp)
			}
		}
	}

	return (*hp)[0]
}

• 另外一个想法就是二分

1. 二分的范围是从差值的范围出发，即 0 -> max(nums) - min(nums)，那么 max min 可以直接排序取首尾即可
2. 但是如何统计，二分中小于 mid 的差值的数量 以 [1,2,2,3,4] 为例，固定右边界为 4 的时候 1 -> 4 中间可能小于 k 的数字组合为 [1,4] [2,4] [2,4] [3,4] 其结果为 j - i = 4 - 0 (4 的下标 4 1 的下标 1)

func smallestDistancePair(nums []int, k int) int {
	if len(nums) == 0 {
		return -1
	}
	sort.Ints(nums)
	// i, j 表示的是 nums 中的 数据差 的范围
	i, j := 0, nums[len(nums)-1] - nums[0]
	for i < j {
		// mid 表示的是中间的差值
		mid := i + (j - i) / 2
		// 找到小于等于 mid 的数值差的数量
		count := findDistancePair(nums, mid)

		if count > k {
			j = mid - 1
		} else if count < k {
			i = mid + 1
		} else {
			// 因为是小于等于 所以可能 mid 是解 也可以是在左边
			j = mid
		}
	}
	return i
}

func findDistancePair(nums []int, distance int) int {
	res := 0
	// 固定右边界
	i, j := 0, 0
	for j < len(nums) {
		// 统计出来的是小于等于 distance 的数量
		for i < j && nums[j] - nums[i] > distance {
			i++
		}
		// 因为是递增的 如果这个时候 1,2,2,3,4 相当于固定右边界 那么排序完的数组 左边能够形成的满足条件的数对 应该是 j - i 个
		res += j - i
		j++
	}
	return res
}

字典树

猜字谜

暴力解法，用 word 去匹配 puzzle 的 set 超时了。

而原题目中 words 的数量比 puzzles 的数量高一个数量级，因此可以使用 字典树 压缩 word 的数量，用 puzzle 进行比较

private class TrieTree {
		int currency;
		TrieTree[] child;

		public TrieTree() {
				this.currency = 0;
				// 因为只包含小写字母
				this.child = new TrieTree[26];
		}

		public void add(char[] word) {
				TrieTree cur = this;

				for (char c : word) {
						if (cur.child[c - 'a'] == null) {
								cur.child[c - 'a'] = new TrieTree();
						}
						cur = cur.child[c - 'a'];
				}
				// currency 表示有一个 word 到达了这个底
				cur.currency++;
		}
}

public List<Integer> findNumOfValidWords(String[] words, String[] puzzles) {
		// 因为实际上并不在意 word 的顺序 而且根据题目要求 word 不定长 而且比 puzzle 大 因为 puzzle 是 7 为固定长度
		// 所以固定 word 为 字符树

		TrieTree root = new TrieTree();
		// 加入字典树中相当于 压缩了 words
		for (String word : words) {
				// 排序去重加入 因为这样才能统计 currency 并进行压缩
				root.add(getCharArray(word));
		}
		List<Integer> res = new ArrayList<>(puzzles.length);
		for (int i = 0; i < puzzles.length; i++) {
				res.add(0);
		}

		// 比较 puzzle 与 字典树
		// puzzle 最大深度为 7
		// 最后只需要加上 currency 即可
		for (int i = 0; i < puzzles.length; i++) {
				char[] puzzleArray = getCharArray(puzzles[i]);
				char required = puzzles[i].charAt(0);
				res.set(i, recursionSearch(root, puzzleArray, 0, required));
		}
		return res;
}

// puzzle 去匹配字典树 找到一个 节点 返回其 currency 即对应的 word 数量
public int recursionSearch(TrieTree node, char[] puzzleArray, int pos, char required) {
		if (node == null) {
				return 0;
		}
		// puzzle 最深就打到这儿
		if (pos == puzzleArray.length) {
				return node.currency;
		}

		// 可以选择用当前 pos 这个位置来匹配 然后都 ++
		int res = recursionSearch(node.child[puzzleArray[pos] - 'a'], puzzleArray, pos + 1, required);
		// 因为去重了 所以 required 等于的时候 一定要匹配

		// 不等于的时候，可以维持 node 引用 然后不匹配 跳过 puzzle 的这个字符 继续往下走
		if (puzzleArray[pos] != required) {
				// + 是因为 可以用多条路走 实际上就是要或者不要
				res += recursionSearch(node, puzzleArray, pos + 1, required);
		}
		return res;
}

public char[] getCharArray(String word) {
		char[] tmp = word.toCharArray();
		Arrays.sort(tmp);
		int newIndex = 0;
		int l = 0, r = 0;
		while (r < tmp.length) {
				while (r < tmp.length && tmp[r] == tmp[l]) {
						r++;
				}
				tmp[newIndex++] = tmp[l];
				l = r;
		}
		char[] res = new char[newIndex];
		System.arraycopy(tmp, 0, res, 0, newIndex);
		return res;
}

计算器

基本计算器

其本质是一个 中值表达式 求值。实际上只需要注意 符号的 优先级即可。（PS：·· 好多细节没注意到 就会 gg）

TODO: 中值表达式 转成 逆波兰表达式

import java.util.Deque;
import java.util.LinkedList;

public class BasicCalculator_224 {

    private int operate(char operator, int n1, int n2) {
        switch (operator) {
            case '+' -> {
                return n1 + n2;
            }
            case '-' -> {
                return n2 - n1;
            }
        }
        return 0;
    }

    // 字符的优先级！！！ TODO: 中值表达式 转 逆波兰表达式


    // 中缀转后缀
    public int calculate(String s) {
        // 只有 数字 + - ( )

        Deque<Integer> number = new LinkedList<>();
        Deque<Character> operators = new LinkedList<>();
        if (s.length() > 0 && s.charAt(0) == '-') {
            s = '0' + s;
        }

        s = s.replaceAll("\\(\\+", "(0+");
        s = s.replaceAll("\\(-", "(0-");
        for (int i = 0; i < s.length(); ) {
            char c = s.charAt(i);

            if (c == ' ') {
                i++;
            } else if (c == '+') {
                // 需要弹出栈 直到优先级相等 因为只有 - + 所以需要一直弹出到 -
                while (operators.size() > 0 && operators.peekLast() != '+' && operators.peekLast() != '(') {
                    int first = number.removeLast();
                    int second = 0;
                    if (!number.isEmpty()) second = number.removeLast();
                    number.add(operate(operators.removeLast(), first, second));
                }
                operators.add(c);
                i++;
            } else if (c == '-') {
                while (operators.size() > 0 && operators.peekLast() == '-' && operators.peekLast() != '(') {
                    int first = number.removeLast();
                    int second = 0;
                    if (!number.isEmpty()) second = number.removeLast();
                    number.add(operate(operators.removeLast(), first, second));
                }
                operators.add(c);
                i++;
            } else if (c == '(') {
                operators.add(c);
                i++;
            } else if (c == ')') {
                // 弹栈
                while (operators.size() > 0 && operators.peekLast() != '(') {
                    int first = number.removeLast();
                    int second = 0;
                    if (!number.isEmpty()) second = number.removeLast();
                    number.add(operate(operators.removeLast(), first, second));
                }
                // 去掉 (
                operators.removeLast();
                i++;
            } else {
                int num = 0;
                // 数字
                while (i < s.length() && s.charAt(i) >= '0' && s.charAt(i) <= '9') {
                    num = num * 10 + s.charAt(i) - '0';
                    i++;
                }
                number.add(num);
            }
        }

        while (!operators.isEmpty()) {
            int first = number.removeLast();
            int second = 0;
            if (!number.isEmpty()) second = number.removeLast();
            number.add(operate(operators.removeLast(), first, second));
        }
        return number.getLast();
    }


    public static void main(String[] args) {
        System.out.println(new BasicCalculator_224().calculate( "(6)-(8)-(7)+(1+(6))"));
        System.out.println(new BasicCalculator_224().calculate( "1 + 1"));
        System.out.println(new BasicCalculator_224().calculate( " 2-1 + 2 "));
        System.out.println(new BasicCalculator_224().calculate( "(1+(4+5+2)-3)+(6+8)"));
    }
}

数学问题

1802. 有界数组中指定下标处的最大值

给你三个正整数 n、index 和 maxSum 。你需要构造一个同时满足下述所有条件的数组 nums（下标 从 0 开始 计数）：
nums.length == n
nums[i] 是 正整数 ，其中 0 <= i < n
abs(nums[i] - nums[i+1]) <= 1 ，其中 0 <= i < n-1
nums 中所有元素之和不超过 maxSum
nums[index] 的值被 最大化
返回你所构造的数组中的 nums[index] 。

这个问题就是说构建一个只有正整数的数组，且相邻数字之间差值不能超过 1，问 如何构建才能使 index 下标位置的数最大。

其实偏向于贪心的策略，既然要 index 最大，那么每次遍历的时候，我都在 index 上 +1，看在没有打到 maxSum 的时候能够给这个地方添加几次。最后其实际的生长过程可以看做下面的一个过程。

例输入：n = 4, index = 2, maxSum = 6

1. 构建基础数组，因为要求每个数字都为正整数，因此最小为 1

1 1 1 1
    _
    |
  index 

2. 从 index 开始生长

    2 

1 1 1 1
    _
    |
  index 

这个时候 已经不能再加 1 了 所以直接返回 2

所以其实就是构建一个题型的台状结构，每层比下一层只会高 1 个，最后到 index 的位置最高即可。

class Solution {
    public int maxValue(int n, int index, int maxSum) {
        // 因为是正整数 所以相当于每个数字至少要填上1
        int remain = maxSum - n;

        // 现在 index 位置填入的是 1
        int res = 1;
        // 然后根据剩下的数字 从 index 开始增加
        int l = index, r = index;

        while (l > 0 || r < n - 1) {
            // 在 l 到 r 之间的数字 加 1
            int len = r - l + 1;
            if (remain >= len) {
                // index 对应位置的数字 一定是在 l,r 之间的
                res += 1;
                // 因为相邻不能相差 1 所以 每次 l、r 向外增加 1 位长度
                l = Math.max(0, l - 1);
                r = Math.min(r + 1, n - 1);
                remain -= len;
            } else {
                break;
            }
        }

        // 还剩下 全部加一
        res += remain / n;
        return res;
    }
}

132 模式

在一个数组中找到下标 i < j < k 满足 nums[i] < nums[k] < nums[j] 也就是说 j 对应的数值 是三个中最大的 k 次之，最小的是 i

那么很容易知道 i 的值其实需要越小越好，越小的话，后面 k、j 的条件就最好满足，因此第一步就是求出从左向右的最小值数组

• brute force 的方法(o(n^2))

既然已经知道 i 取从左向右的最小值，那么只想就需要确定 j < k 且 nums[i] < nums[k] < nums[j]，也就是在后续的数组中找到一对逆序的数组，那么 o(n^2) 的算法就很好写了

// 找到 1 3 2 模式
// bruteforce 的方法 因为要找到 i < j < k 满足 nums[i] < nums[k] < nums[j] 的格式
// 即中间的数是最大 那么 nums[i] 一定是最小 所以先维护一个 leftMin 表示从左侧开始的最小值
// 然后开始遍历数组 找到一个 逆序数对 且逆序数对中的最小值 大于 leftMin 的值 即可找到
// 所以是 o(n^2)
public boolean find132patternBruteForce(int[] nums) {
		if (nums == null || nums.length < 3) return false;

		int[] leftMin = new int[nums.length];
		leftMin[0] = nums[0];
		for (int i = 1; i < nums.length; i++) {
				leftMin[i] = Math.min(leftMin[i - 1], nums[i]);
		}

		// 先固定一个最小值
		// 然后在找到一个逆序的点
		for (int i = 1; i < nums.length - 1; i++) {
				for (int j = i + 1; j < nums.length; j++) {
						if (nums[j] > leftMin[i] && nums[i] > nums[j]) return true;
				}
		}

		return false;
}

• 优化的算法（o(n)）

之前的算法寻找逆序的时候，是在确定了 j 值 的情况下从前向后寻找 k 值，如果能够知道之前访问的过的 j 值，作为当前 k 值，那么就可以进一步的降低复杂度。

因为，在满足 nums[j] > leftMin[j] (即 nums[i]) 时，如果 k 值正好取到小于 nums[j] 的值 且 大于 nums[i] 时满足条件。所以 nums[k] 的值 在取小于 nums[j] 的值的时候 越大越好，因为这样才可能更大程度的满足 nums[k] > nums[i] 的条件。

所以使用一个单调栈来保存 j 之后遍历的历史情况，越靠近栈底的值越大，只需要取到栈中需要的满足小于 nums[j] 的最大值即可。

这样 栈中还保存着较大的值，之后再遍历的时候，还以用这个比 nums[j] 大的值，与 j 之前更大的值匹配成 132 组合。 而 j 之后的较小值，如何满足题设条件，会在第一次访问的时候就返回了，所以也不会存在漏的结果。

public boolean find132pattern(int[] nums) {
		if (nums == null || nums.length < 3) return false;

		int[] leftMin = new int[nums.length];
		leftMin[0] = nums[0];
		for (int i = 1; i < nums.length; i++) {
				leftMin[i] = Math.min(leftMin[i - 1], nums[i]);
		}
		Deque<Integer> stack = new LinkedList<>();

		// 从后向前找 因为要找的是 j < k nums[j] > nums[k] 的结果
		// 那么只需要保存遍历的 j 之后的比 nums[j] 小 且比 leftMin 大的最大值 这样就可以满足要求了
		// 所以 stack 中保存的是 j 之后的 较大的值 如果能够在其中找到一个小于 nums[j] 的值 就证明可行
		for (int j = nums.length - 1; j >= 0; j--) {
				// 必须要比左侧最小的大 才能比较
				if (nums[j] > leftMin[j]) {
						// 因为要在 j 右边找一个更小的 nums[k] 所以 比 nums[j] 小的 都出栈
						// 比较其中的最大值与 leftMin 的大小既可以知道
						int remove = Integer.MIN_VALUE;
						while (!stack.isEmpty() && stack.peekLast() < nums[j]) {
								remove = stack.removeLast();
						}
						if (remove > leftMin[j]) return true;
						stack.addLast(nums[j]);
				}
		}
		return false;
}

最大子序和

简单的题型

简单的题型如 剑指offer 上所述，只需要用一个数组保存以当前结尾的最大子序和即可。转移的时候，如果之前的最大子序和小于 0，说明应该重新开始计数。

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < nums.length; i++) {
            if (i == 0 || dp[i - 1] < 0) {
                dp[i] = nums[i];
            } else {
                dp[i] = dp[i - 1] + nums[i];
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

删除一次得到子数组最大和

• 直觉想法

拿到这个题目的第一个直觉就是跟上面那个基本一致，但是需要删除一个数字，那么删除的这个数字一定存在这样的性质。

删除这个数字后，有可能左右的最大子序和加起来更大，所以这个数字一定是负数。

那么，只需要知道这个数字左边和右边的分别的最大子序和即可，那么就可以用两次上面的算法，得到以 i 结尾的从左向右最大子序和 和 以 i 结尾的从右想左的最大子序和即可

// 最大子序和的变种 如果中间可以删除一个数字 问能够形成的最大子序和为多少
public int maximumSumWithTwoDirection(int[] arr) {
		if (arr == null || arr.length == 0) return 0;
		if (arr.length == 1) return arr[0];

		// 因此要删除一个的话 只需要遍历被删除的项即可，然后将以 arr[i] 结尾的左右的最大子序和累加起来即可
		int[] left = new int[arr.length + 1];
		int[] right = new int[arr.length + 1];

		for (int i = 0; i < arr.length; i++) {
				if (left[i] < 0) left[i + 1] = arr[i];
				else left[i + 1] = left[i] + arr[i];
		}

		for (int j = arr.length - 1; j >= 0; j--) {
				if (right[j + 1] < 0) right[j] = arr[j];
				else right[j] = right[j + 1] + arr[j];
		}

		int res = Math.max(left[arr.length], right[0]);
		// 遍历需要删除的负数点 因为只有负数才需要删除 删除后才可能达到需要的连续两个段的最大值
		for (int i = 0; i < arr.length; i++) {
				// 只有小于 0 才需要分隔
				if (arr[i] < 0) {
						// 注意的是需要分离开 i == 0 i == arr.length - 1 因为 默认是0 会影响 res 为负数的情况
						if (i == 0) {
								res = Collections.max(Arrays.asList(right[i + 1], res));
						} else if (i == arr.length - 1) {
								res = Collections.max(Arrays.asList(left[i], res));
						} else {
								// 平时的话 去掉这个值 只需要在三部分中取较大值与 res 比较即可
								res = Collections.max(Arrays.asList(left[i] + right[i + 1], left[i], right[i + 1], res));
						}
				}
		}
		// 没有小于 0 的话 说明全是正数
		// 返回和即可
		return res;
}

• 两个 dp 数组保存状态

那么可以使用一个循环得到结果。

1. 仍然需要一个数组保存以 arr[i] 结尾时的最大子序和
2. 需要一个数组保存以 arr[i] 结尾时删除一个数字的最大子序和

那么删除的这个数字可能是遍历的 arr[i] 或者 之前就已经删除了一个数字，arr[i] 不能被删除。所以第2个数组的更新策略即deleteOne[i] = Math.max(deleteOne[i - 1] + arr[i], dp[i - 1])。

即保留当前的 arr[i] 那么只能取之前删除了一次的最大子序和 和 删除当前的 arr[i]，那么就要去之前没有删除数字的最大子序和 dp[i - 1]。

public int maximumSum(int[] arr) {
		if (arr == null || arr.length == 0) return 0;

		int[] dp = new int[arr.length];
		// 保存删除一个的结果
		int[] deleteOne = new int[arr.length];

		dp[0] = arr[0];
		// 最小值到达 -10^ (4)
		deleteOne[0] = -100000;
		int res = Math.max(dp[0], deleteOne[0]);
		for (int i = 1; i < arr.length; i++) {
				dp[i] = Math.max(arr[i], dp[i - 1] + arr[i]);
				// 要删除一个数的话 要么保留当前数 和 之前删除一个数形成的最大值比较 要么删除当前这个数 与之前保存的最大值比较
				deleteOne[i] = Math.max(deleteOne[i - 1] + arr[i], dp[i - 1]);
				res = Math.max(res, Math.max(dp[i], deleteOne[i]));
		}
		return res;
}